
分析 (1)利用三角恒等变换化简函数的解析式,再利用正弦函数的周期性,求得该函数的周期.
(2)利用正弦函数的定义域和值域,求得函数在区间$[{-\frac{π}{4},\frac{π}{3}}]$上的最大值和最小值及取得最大、最小值时对应的x值.
解答 解:(1)∵$f(x)=4cosx(\frac{1}{2}sinx-\frac{{\sqrt{3}}}{2}cosx)+\sqrt{3}=2sinxcosx-2\sqrt{3}{cos^2}x+\sqrt{3}$
=$sin2x-\sqrt{3}cos2x$=$2sin(2x-\frac{π}{3})$,
故该函数的周期为$\frac{2π}{2}$=π.
(2)在区间$[{-\frac{π}{4},\frac{π}{3}}]$上,2x-$\frac{π}{3}$∈[-$\frac{5π}{6}$,$\frac{π}{3}$],
则当2x-$\frac{π}{3}$=$\frac{π}{3}$,即$x=\frac{π}{3}$时,函数取得最大值$\sqrt{3}$;
当2x-$\frac{π}{3}$=-$\frac{π}{2}$,即$x=-\frac{π}{12}$时,函数取得最小值-2.
点评 本题主要考查三角恒等变换,正弦函数的周期性,正弦函数的定义域和值域,属于中档题.


 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | A∩B={-2,-1} | B. | (∁RA)∪B=(-∞,0) | C. | A∪B=(0,+∞) | D. | (∁RA)∩B={-2,-1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | 1 | C. | $\frac{{2\sqrt{10}}}{5}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
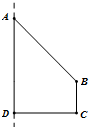 如图,在四边形ABCD中,AD⊥DC,AD∥BC,AD=3,CD=2,$AB=2\sqrt{2}$,∠DAB=45°,四边形绕着直线AD旋转一周,
如图,在四边形ABCD中,AD⊥DC,AD∥BC,AD=3,CD=2,$AB=2\sqrt{2}$,∠DAB=45°,四边形绕着直线AD旋转一周,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com