
分析 将元素a、b、c、d和1、2、3、4、5、6分别按从小到大的顺序排列,然后按照象的个数分类讨论得答案.
解答 解:将元素a、b、c、d和1、2、3、4、5、6分别按从小到大的顺序排列.
(1)只有一个象的映射有C61=6个;
(2)若恰有两个象,就先选出两个象,再把a,b,c,d用插空法分成两段,
并按照原顺序对应,有C31•C62=45个;
(3)若恰有三个象,就先选出三个象,将a,b,c,d用插空法分为三段,
并按照原顺序对应,有C32$•{C}_{6}^{3}$=60个;
(4)若恰有四个象,就选出四个象共C64=15个.
综上知,适合条件的映射共有6+45+60+15=126个.
点评 本题主要考查映射、排列组合等基础知识,考查运算求解能力,考查分类讨论思想、化归与转化思想,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=y | B. | x+y=1 | C. | $|{\overrightarrow b}|y=|{\overrightarrow a}|x$ | D. | $|{\overrightarrow a}|y=|{\overrightarrow b}|x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在x∈R,使得ex≤0 | |
| B. | “x>1”是“x>2”的充分不必要条件 | |
| C. | x+$\frac{1}{x}$≥2对任意正实数x恒成立 | |
| D. | “p或q是假命题”“¬p为真命题”的必要不充分条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
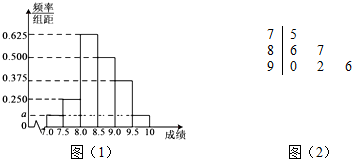 某县电视台决定于2015年元旦前夕举办“弘扬核心价值观,激情唱响中国梦”全县歌手大奖赛,比赛分初赛演唱部分和决赛问答题部分,各位选手的演唱部分成绩频率分布直方分布图(1)如图:已知某工厂的6名参赛人员的演唱成绩得分(满分10分)如茎叶图(2)(茎上的数字为整数部分,叶上的数字为小数部分).
某县电视台决定于2015年元旦前夕举办“弘扬核心价值观,激情唱响中国梦”全县歌手大奖赛,比赛分初赛演唱部分和决赛问答题部分,各位选手的演唱部分成绩频率分布直方分布图(1)如图:已知某工厂的6名参赛人员的演唱成绩得分(满分10分)如茎叶图(2)(茎上的数字为整数部分,叶上的数字为小数部分).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com