
| A. | x=y | B. | x+y=1 | C. | $|{\overrightarrow b}|y=|{\overrightarrow a}|x$ | D. | $|{\overrightarrow a}|y=|{\overrightarrow b}|x$ |
分析 做出平行四边形ODCE,则四边形ODCE为菱形,于是|OD|=|OE|,从而得出结论.
解答 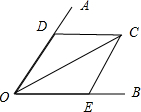 解:以OA,OB的方向为邻边方向,以OC为对角线做平行四边形ODCE,
解:以OA,OB的方向为邻边方向,以OC为对角线做平行四边形ODCE,
则$\overrightarrow{OC}$=$\overrightarrow{OD}$+$\overrightarrow{OE}$,
∵$\overrightarrow{OC}=x\overrightarrow a+y\overrightarrow b$,
∴$\overrightarrow{OD}$=x$\overrightarrow{a}$,$\overrightarrow{OE}$=y$\overrightarrow{b}$,x>0,y>0.
∵OC平分∠AOB,∴平行四边形ODCE是菱形.
∴|OD|=|OE|,
∴x|$\overrightarrow{a}$|=y|$\overrightarrow{b}$|,
故选C.
点评 本题考查了平面向量的基本道理,向量线性运算的几何意义,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\int_0^1{[{{{(tanx)}^{11}}+{{(cosx)}^{21}}}]dx}$ | B. | 0 | ||
| C. | $2\int_0^1{{{(cosx)}^{21}}dx}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{7}{9}$ | C. | -$\frac{1}{9}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 今年来空气污染是一个生活中重要的话题,PM2.5就是其中一个指标,PM2.5指大气总直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,PM2.5日均值在35毫克/立方米以下空气质量为一级;在35毫克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标,某地区2014年12月1日至10日每天的PM2.5检测数据如茎叶图所示:
今年来空气污染是一个生活中重要的话题,PM2.5就是其中一个指标,PM2.5指大气总直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,PM2.5日均值在35毫克/立方米以下空气质量为一级;在35毫克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标,某地区2014年12月1日至10日每天的PM2.5检测数据如茎叶图所示:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com