
分析 ①把甲、乙、丙三人合格的概率相乘,即得所求.
②在甲、乙、丙三人中,求出其中仅有2个人合格、一个人不合格的概率,再相加,即得所求.
③先求出甲、乙、丙三人都不合格的概率,再用1减去此概率,即为所求.
解答 解:①由题意甲、乙、丙三人合格的概率分别为$\frac{3}{5},\frac{3}{4},\frac{1}{3}$,
可得三人都合格的概率为$\frac{3}{5}•\frac{3}{4}•\frac{1}{3}$=$\frac{3}{20}$.
②有2人合格的概率为$\frac{3}{5}•\frac{3}{4}•(1-\frac{1}{3})$+$\frac{3}{5}•(1-\frac{3}{4})•\frac{1}{3}$+(1-$\frac{3}{5}$)•$\frac{3}{4}•\frac{1}{3}$=$\frac{3}{10}$+$\frac{1}{20}$+$\frac{1}{10}$=$\frac{9}{20}$.
③甲、乙、丙三人都不合格的概率为$\frac{2}{5}•\frac{1}{4}•\frac{2}{3}$=$\frac{1}{15}$,
∴甲、乙、丙三人至少有一个合格的概率为1-$\frac{1}{15}$.
点评 本题主要考查相互独立事件的概率乘法公式,所求的事件与它的对立事件概率间的关系,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
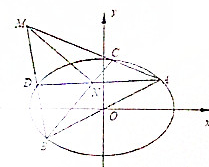 已知直线y=$\frac{1}{2}$x与椭圆E:x2+2y2=λ(λ>0)交于A,B两点,C,D是椭圆E上异于A,B的两点且直线AC,BD交于M,AD,BC交于点N,试求直线MN的斜率.
已知直线y=$\frac{1}{2}$x与椭圆E:x2+2y2=λ(λ>0)交于A,B两点,C,D是椭圆E上异于A,B的两点且直线AC,BD交于M,AD,BC交于点N,试求直线MN的斜率.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=y | B. | x+y=1 | C. | $|{\overrightarrow b}|y=|{\overrightarrow a}|x$ | D. | $|{\overrightarrow a}|y=|{\overrightarrow b}|x$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com