
分析 本题考查的知识点是设计程序框图解决实际问题,我们根据题目已知中分段函数的解析式f(x)=$\left\{\begin{array}{l}{{x}^{2}-1,x<0}\\{5x,0≤x<1}\\{x+7,x≥1}\end{array}\right.$,然后根据分类标准,设置两个判断框的并设置出判断框中的条件,再由函数各段的解析式,确定判断框的“是”与“否”分支对应的操作,由此即可画出流程图,再编写满足题意的程序.
解答 解:算法框图如下所示: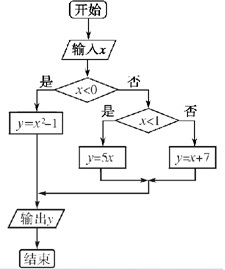
算法语句如下:
INPUT x
IF x<0 THEN y=x^2-1
ELSE
IF x<1 THEN
y=5*x
ELSE
y=x+7
END IF
END IF
PRINT y
END
点评 本题考查了设计程序框图解决实际问题.主要考查编写伪代码程序解决分段函数问题,属于基础题.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:选择题
| A. | k<-1 | B. | k≤-1 | C. | k>2 | D. | k≥2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+3i | B. | 1-3i | C. | 3i | D. | -3i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\int_0^1{[{{{(tanx)}^{11}}+{{(cosx)}^{21}}}]dx}$ | B. | 0 | ||
| C. | $2\int_0^1{{{(cosx)}^{21}}dx}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com