
分析 (1)在等差数列{an}中,由已知求得公差,代入等差数列的通项公式得答案;
(2)由bn+$\sqrt{2}$=an,得${b}_{n}={a}_{n}-\sqrt{2}=2n$,结合数列{${b}_{{n}_{k}}$}是等比数列即可求得${n}_{k}={3}^{k-1}$;
(3)假设存在三项ar,as,at成等比数列,则${{a}_{s}}^{2}={a}_{r}{a}_{t}$,即有$(2s+\sqrt{2})^{2}=(2r+\sqrt{2})(2t+\sqrt{2})$,整理后分rt-s2≠0和rt-s2=0推得矛盾,可知不存在满足题意的三项ar,as,at.
解答 解:(1)在等差数列{an}中,
∵a1=2+$\sqrt{2}$,S3=12+3$\sqrt{2}$,∴$3{a}_{1}+3d=12+3\sqrt{2}$,得d=2,
∴${a}_{n}={a}_{1}+(n-1)d=2n+\sqrt{2}$,${S}_{n}=\frac{n({a}_{1}+{a}_{n})}{2}={n}^{2}+(\sqrt{2}+1)n$;
(2)∵bn+$\sqrt{2}$=an,∴${b}_{n}={a}_{n}-\sqrt{2}=2n$,
∴${b}_{{n}_{k}}=2{n}_{k}$,又数列{${b}_{{n}_{k}}$}的首项为${b}_{{n}_{1}}={b}_{1}=2$,公比q=$\frac{{b}_{3}}{{b}_{1}}=3$,
∴${b}_{{n}_{k}}=2•{3}^{k-1}$,则$2{n}_{k}=2{3}^{k-1}$,故${n}_{k}={3}^{k-1}$;
(3)假设存在三项ar,as,at成等比数列,则${{a}_{s}}^{2}={a}_{r}{a}_{t}$,
即有$(2s+\sqrt{2})^{2}=(2r+\sqrt{2})(2t+\sqrt{2})$,
整理得:$(rt-{s}^{2})\sqrt{2}=2s-r-t$,若rt-s2≠0,则$\sqrt{2}=\frac{2s-r-t}{rt-{s}^{2}}$,
∵r,s,t∈N*,∴$\frac{2s-r-t}{rt-{s}^{2}}$是有理数,与$\sqrt{2}$为无理数矛盾;
若rt-s2=0,则2s-r-t=0,从而可得r=s=t,这样r<s<t矛盾.
综上可知,不存在满足题意的三项ar,as,at.
点评 本题考查数列递推式,考查了等差数列和等比数列的通项公式,训练了存在性问题的求解方法,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| 广告费用x(万元) | 3 | 4 | 5 |
| 销售额y(万元) | 22 | 28 | m |
| A. | 40 | B. | 39 | C. | 38 | D. | 37 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
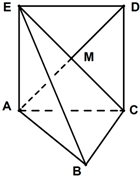 如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC.
如图,正方形ACDE所在的平面与平面ABC垂直,M是CE和AD的交点,AC⊥BC,且AC=BC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
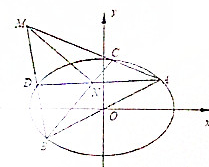 已知直线y=$\frac{1}{2}$x与椭圆E:x2+2y2=λ(λ>0)交于A,B两点,C,D是椭圆E上异于A,B的两点且直线AC,BD交于M,AD,BC交于点N,试求直线MN的斜率.
已知直线y=$\frac{1}{2}$x与椭圆E:x2+2y2=λ(λ>0)交于A,B两点,C,D是椭圆E上异于A,B的两点且直线AC,BD交于M,AD,BC交于点N,试求直线MN的斜率.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com