
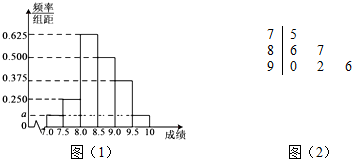
 某县电视台决定于2015年元旦前夕举办“弘扬核心价值观,激情唱响中国梦”全县歌手大奖赛,比赛分初赛演唱部分和决赛问答题部分,各位选手的演唱部分成绩频率分布直方分布图(1)如图:已知某工厂的6名参赛人员的演唱成绩得分(满分10分)如茎叶图(2)(茎上的数字为整数部分,叶上的数字为小数部分).
某县电视台决定于2015年元旦前夕举办“弘扬核心价值观,激情唱响中国梦”全县歌手大奖赛,比赛分初赛演唱部分和决赛问答题部分,各位选手的演唱部分成绩频率分布直方分布图(1)如图:已知某工厂的6名参赛人员的演唱成绩得分(满分10分)如茎叶图(2)(茎上的数字为整数部分,叶上的数字为小数部分).分析 (1)利用概率和为1,求出a,即可得出结论;
(2)确定X的取值为3,4,5,求出相应的概率,即可求X的分布列及X的数学期望.
解答 解:(1)由题意(2a+0.25+0.375+0.5+0.625)×0.5=1,
∴a=0.125,(2分)
全部参赛人员的整体水平为(0.125×$\frac{7.0+7.5}{2}$+0.25×$\frac{7.5+8.0}{2}$+0.625×$\frac{8.0+8.5}{2}$+0.5×$\frac{8.5+9.0}{2}$+0.375×$\frac{9.0+9.5}{2}$+0.125×$\frac{9.5+10}{2}$)×0.5≈8.531.(4分)
根据茎叶图估计,中位数为8.85,数据集中在9.0以上,
所以某工厂的参赛6名人员的演唱水平显然高于全部参赛人员的平均水平.(5分)
(2)从这6位抽取2位的基本事件总数为C${\;}_{6}^{2}$,分差大于0.5的基本事件为除数据(8.6,8.7),(8.6,9.0),(9.2,9.6),(9.2,9.0),(8.7,9.0),(9.2,8.7)外的9个基本事件,故概率为P=$\frac{9}{{C}_{6}^{2}}$=$\frac{3}{5}$.(7分)
依题意,X的取值为3,4,5,则P(X=3)=$(\frac{3}{5})^{3}+(\frac{2}{5})^{2}$=$\frac{35}{125}$;
P(X=4)=${C}_{3}^{2}•(\frac{3}{5})^{2}•\frac{2}{5}•\frac{3}{5}$+${C}_{3}^{2}•(\frac{2}{5})^{2}•\frac{3}{5}•\frac{2}{5}$=$\frac{234}{2{5}^{2}}$;
P(X=5)=${C}_{4}^{2}•(\frac{3}{5})^{2}•(\frac{2}{5})^{2}•\frac{3}{5}$+${C}_{4}^{2}•(\frac{2}{5})^{2}•(\frac{3}{5})^{2}•\frac{2}{5}$=$\frac{216}{2{5}^{2}}$.(10分)
| X | 3 | 4 | 5 |
| P | $\frac{35}{125}$ | $\frac{234}{2{5}^{2}}$ | $\frac{216}{2{5}^{2}}$ |
点评 本题考查频率分布直方分布图,考查茎叶图,考查分布列与期望的计算,考查学生分析解决问题的能力,属于中档题.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
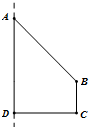 如图,在四边形ABCD中,AD⊥DC,AD∥BC,AD=3,CD=2,$AB=2\sqrt{2}$,∠DAB=45°,四边形绕着直线AD旋转一周,
如图,在四边形ABCD中,AD⊥DC,AD∥BC,AD=3,CD=2,$AB=2\sqrt{2}$,∠DAB=45°,四边形绕着直线AD旋转一周,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 今年来空气污染是一个生活中重要的话题,PM2.5就是其中一个指标,PM2.5指大气总直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,PM2.5日均值在35毫克/立方米以下空气质量为一级;在35毫克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标,某地区2014年12月1日至10日每天的PM2.5检测数据如茎叶图所示:
今年来空气污染是一个生活中重要的话题,PM2.5就是其中一个指标,PM2.5指大气总直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,PM2.5日均值在35毫克/立方米以下空气质量为一级;在35毫克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标,某地区2014年12月1日至10日每天的PM2.5检测数据如茎叶图所示:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2π}$ | B. | $\frac{1}{π}$ | C. | $\frac{2}{π}$ | D. | $\frac{1}{3π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1006 | B. | 2012 | C. | 22012 | D. | 2-2012 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com