
| A. | 1006 | B. | 2012 | C. | 22012 | D. | 2-2012 |
分析 根据平面向量的基本定理得出a7+a2006=1,再利用等差数列的性质与前n项和公式,即可求出S2012的值.
解答 解:∵$\overrightarrow{OB}$=a7$\overrightarrow{OA}$+a2006$\overrightarrow{OC}$,且A、B、C三点共线(该直线不过点O),
∴a7+a2006=1;
∵数列{an}是等差数列,
∴a1+a2012=a7+a2006;
∴S2012=$\frac{2012×{(a}_{1}{+a}_{2012})}{2}$=1006.
故选:A.
点评 本题考查了平面向量的基本定理与等差数列的性质、前n项和公式的应用问题,是基础题目.


科目:高中数学 来源: 题型:解答题
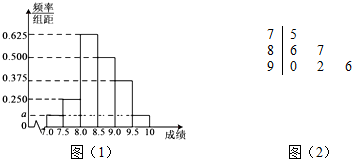 某县电视台决定于2015年元旦前夕举办“弘扬核心价值观,激情唱响中国梦”全县歌手大奖赛,比赛分初赛演唱部分和决赛问答题部分,各位选手的演唱部分成绩频率分布直方分布图(1)如图:已知某工厂的6名参赛人员的演唱成绩得分(满分10分)如茎叶图(2)(茎上的数字为整数部分,叶上的数字为小数部分).
某县电视台决定于2015年元旦前夕举办“弘扬核心价值观,激情唱响中国梦”全县歌手大奖赛,比赛分初赛演唱部分和决赛问答题部分,各位选手的演唱部分成绩频率分布直方分布图(1)如图:已知某工厂的6名参赛人员的演唱成绩得分(满分10分)如茎叶图(2)(茎上的数字为整数部分,叶上的数字为小数部分).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
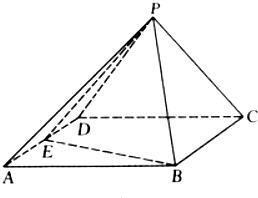 如图,四棱锥P-ABCD的底面ABCD是菱形,∠DAB=60°,E是AD的中点,PA=PD.
如图,四棱锥P-ABCD的底面ABCD是菱形,∠DAB=60°,E是AD的中点,PA=PD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{π}$ | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com