
分析 根据集合的基本运算以及充分条件和必要条件的定义进行判断即可.
解答 解:∵A∩B={$\frac{1}{2}$},∴sinθ=$\frac{1}{2}$,
则当θ=$\frac{π}{6}$时,也满足条件,
故必要性不成立,
若θ=$\frac{5π}{6}$,则sinθ=sin $\frac{5π}{6}$=$\frac{1}{2}$,
则A={1,$\frac{1}{2}$},满足A∩B={$\frac{1}{2}$},即充分性成立,
故“θ=$\frac{5π}{6}$”是“A∩B={$\frac{1}{2}$}”的充分不必要条件,
故答案为:充分不必要.
点评 本题主要考查充分条件和必要条件的判断,根据集合的基本运算结合充分条件和必要条件的定义是解决本题的关键.比较基础.


科目:高中数学 来源: 题型:解答题
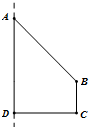 如图,在四边形ABCD中,AD⊥DC,AD∥BC,AD=3,CD=2,$AB=2\sqrt{2}$,∠DAB=45°,四边形绕着直线AD旋转一周,
如图,在四边形ABCD中,AD⊥DC,AD∥BC,AD=3,CD=2,$AB=2\sqrt{2}$,∠DAB=45°,四边形绕着直线AD旋转一周,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2π}$ | B. | $\frac{1}{π}$ | C. | $\frac{2}{π}$ | D. | $\frac{1}{3π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$ | B. | 3 | C. | -3 | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1006 | B. | 2012 | C. | 22012 | D. | 2-2012 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
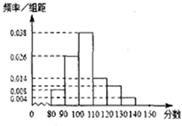 对某文科班50名同学的一次数学成绩进行了统计,全年级文科数学平均分是100分,这个班数学成绩的频率分布直方图如图:(总分150分)从这个班中任取1人,其数学成绩达到或超过年级文科平均分的概率是0.66.
对某文科班50名同学的一次数学成绩进行了统计,全年级文科数学平均分是100分,这个班数学成绩的频率分布直方图如图:(总分150分)从这个班中任取1人,其数学成绩达到或超过年级文科平均分的概率是0.66.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com