
分析 (1)根据平面向量的数量积计算f(x),利用最小正周期求出ω的值,写出f(x)的解析式,再求出f(x)的单调增区间;
(2)根据x的取值范围求出2x+$\frac{π}{3}$的取值范围,再求sin(2x+$\frac{π}{3}$)的取值范围即可.
解答 解:(1)∵向量$\overrightarrow{m}$=(2sin(ωx+$\frac{π}{3}$),1),$\overrightarrow{n}$=(2cosωx,-$\sqrt{3}$)(ω>0),
∴f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$
=4sin(ωx+$\frac{π}{3}$)cosωx-$\sqrt{3}$
=2sinωxcosωx+2$\sqrt{3}$cos2ωx-$\sqrt{3}$
=sin2ωx+$\sqrt{3}$cos2ωx
=2sin(2ωx+$\frac{π}{3}$),
∴最小正周期为T=$\frac{2π}{2ω}$=π,
解得ω=1,
∴f(x)=2sin(2x+$\frac{π}{3}$);
由2kπ-$\frac{π}{2}$≤2x+$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,k∈Z,
得kπ-$\frac{5π}{12}$≤x≤kπ+$\frac{π}{12}$,k∈Z,
∴f(x)的单调递增区间是[kπ-$\frac{5π}{12}$,kπ+$\frac{π}{12}$],k∈Z,
(Ⅱ)∵x∈[-$\frac{5π}{6}$,$\frac{π}{12}$],∴2x+$\frac{π}{3}$∈[-$\frac{4π}{3}$,$\frac{π}{2}$],
∴sin(2x+$\frac{π}{3}$)∈[-1,1],
∴f(x)∈[-2,2],
即f(x)的值域是[-2,2].
点评 本题考查了平面向量的数量积与正弦函数的单调性和最值的计算问题,是基础题目.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:解答题
| 指数API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | >300 |
| 空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中重度污染 | 重度污染 |
| 天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
| 非重度污染 | 重度污染 | 合计 | |
| 供暖季 | |||
| 非供暖季节 | |||
| 合计 | 100 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 384 | B. | 768 | C. | -$\frac{3}{512}$ | D. | -$\frac{3}{1024}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
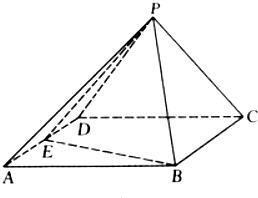 如图,四棱锥P-ABCD的底面ABCD是菱形,∠DAB=60°,E是AD的中点,PA=PD.
如图,四棱锥P-ABCD的底面ABCD是菱形,∠DAB=60°,E是AD的中点,PA=PD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com