
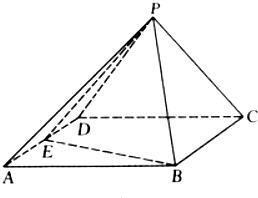
 如图,四棱锥P-ABCD的底面ABCD是菱形,∠DAB=60°,E是AD的中点,PA=PD.
如图,四棱锥P-ABCD的底面ABCD是菱形,∠DAB=60°,E是AD的中点,PA=PD.分析 (1)利用菱形、等边三角形与等腰三角形的性质可得:BE⊥AD,PE⊥AD.再利用线面垂直的性质定理即可得出.
(2)利用面面垂直的性质定理可得:PB⊥平面ABCD,又EB⊥BC.可以建立空间直角坐标系.不妨设BC=2,设平面PCD的法向量为$\overrightarrow{m}$=(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{CP}=0}\\{\overrightarrow{m}•\overrightarrow{CD}=0}\end{array}\right.$,取平面PBC的法向量$\overrightarrow{n}$=(0,1,0),利用cos$<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$即可得出.
解答 (1)证明:连接DB,∵AD=AB,∠DAB=60°,∴△ABD是等边三角形.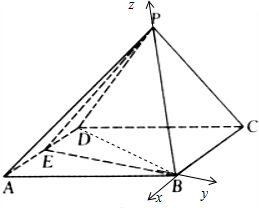
∵E是AD的中点,∴BE⊥AD.
又PA=PD,∴PE⊥AD.
又PE∩BE=E,∴AD⊥平面PBE.
又AD?平面ABCD,
∴平面PBE⊥平面ABCD.
(2)解:平面PBE⊥平面ABCD,平面PBC⊥平面ABCD,平面PBE∩平面PBC=PB,
则PB⊥平面ABCD,∴PB⊥BE,PB⊥BC,又EB⊥BC.
可以建立空间直角坐标系.
不妨设BC=2,则B(0,0,0),C(-2,0,0),P(0,0,2),D(-1,-$\sqrt{3}$,0),
$\overrightarrow{CP}$=(2,0,2),$\overrightarrow{CB}$=(2,0,0),$\overrightarrow{CD}$=(1,-$\sqrt{3}$,0),
设平面PCD的法向量为$\overrightarrow{m}$=(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{CP}=0}\\{\overrightarrow{m}•\overrightarrow{CD}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{2x+2z=0}\\{x-\sqrt{3}y=0}\end{array}\right.$,取$\overrightarrow{m}$=$(\sqrt{3},1,-\sqrt{3})$.
取平面PBC的法向量$\overrightarrow{n}$=(0,1,0),
则cos$<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{1}{\sqrt{7}×1}$=$\frac{\sqrt{7}}{7}$.
点评 本题考查了线面面面垂直的判定与性质定理、菱形与等腰及其等边三角形的性质、向量的夹角公式、法向量的应用,考查了推理能力与计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
 今年来空气污染是一个生活中重要的话题,PM2.5就是其中一个指标,PM2.5指大气总直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,PM2.5日均值在35毫克/立方米以下空气质量为一级;在35毫克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标,某地区2014年12月1日至10日每天的PM2.5检测数据如茎叶图所示:
今年来空气污染是一个生活中重要的话题,PM2.5就是其中一个指标,PM2.5指大气总直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,PM2.5日均值在35毫克/立方米以下空气质量为一级;在35毫克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米以上空气质量为超标,某地区2014年12月1日至10日每天的PM2.5检测数据如茎叶图所示:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
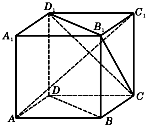
| A. | 异面直线AD与CB1角为60° | B. | BD∥平面CB1D1 | ||
| C. | AC1⊥BD | D. | AC1⊥平面CB1D1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1006 | B. | 2012 | C. | 22012 | D. | 2-2012 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | $({\frac{1}{2},+∞})$ | C. | (-∞,2) | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2),(3) | B. | (1),(3) | C. | (1),(4) | D. | (2),(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com