
| A. | (2),(3) | B. | (1),(3) | C. | (1),(4) | D. | (2),(4) |
分析 由a1>1,a2016a2017>1,$\frac{{a}_{2016}-1}{{a}_{2017}-1}<0$,可得:a2016>1,a2017<1.可得:(1)0<q<1;(2)a2016a2018=${a}_{2017}^{2}$<1;(3)T2016是数列{Tn}中的最大项;(4)T4032=$({a}_{1}{a}_{4032})^{2016}$=$({a}_{2016}{a}_{2017})^{2016}$>1,T4033=$({{a}^{2}}_{2017})^{2016}$×a2017<1,即可得出使Tn>1成立的最大自然数等于4032,即可得出.
解答 解:∵a1>1,a2016a2017>1,$\frac{{a}_{2016}-1}{{a}_{2017}-1}<0$,
∴a2016>1,a2017<1.
∴(1)0<q<1,故正确;
(2)a2016a2018=${a}_{2017}^{2}$<1,故不正确;
(3)T2016是数列{Tn}中的最大项,故正确;
(4)T4032=a1a2•…•a4030a4031•a4032=$({a}_{1}{a}_{4032})^{2016}$=$({a}_{2016}{a}_{2017})^{2016}$>1,
T4033=a1a2•…•a4030a4031•a4032•a4033=$({{a}^{2}}_{2017})^{2016}$×a2017<1,
∴使Tn>1成立的最大自然数等于4032,故不正确.
故选:B.
点评 本题考查了等比数列的通项公式及其性质、递推关系、不等式的性质,考查了推理能力与计算能力,属于中档题.


 巧学巧练系列答案
巧学巧练系列答案 课课练江苏系列答案
课课练江苏系列答案科目:高中数学 来源: 题型:选择题
| A. | 384 | B. | 768 | C. | -$\frac{3}{512}$ | D. | -$\frac{3}{1024}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
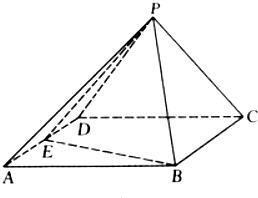 如图,四棱锥P-ABCD的底面ABCD是菱形,∠DAB=60°,E是AD的中点,PA=PD.
如图,四棱锥P-ABCD的底面ABCD是菱形,∠DAB=60°,E是AD的中点,PA=PD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{e}$) | B. | (0,$\frac{1}{2e}$) | C. | [$\frac{ln3}{3}$,$\frac{1}{2e}$) | D. | [$\frac{ln3}{3}$,$\frac{1}{e}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{π}$ | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
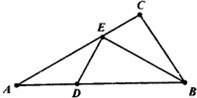 如图,在Rt△ABC中,∠C=90°,BE平分∠ABC,交AC于点E,过点E作ED⊥BE交AB于点D.
如图,在Rt△ABC中,∠C=90°,BE平分∠ABC,交AC于点E,过点E作ED⊥BE交AB于点D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com