
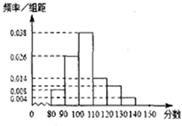
 对某文科班50名同学的一次数学成绩进行了统计,全年级文科数学平均分是100分,这个班数学成绩的频率分布直方图如图:(总分150分)从这个班中任取1人,其数学成绩达到或超过年级文科平均分的概率是0.66.
对某文科班50名同学的一次数学成绩进行了统计,全年级文科数学平均分是100分,这个班数学成绩的频率分布直方图如图:(总分150分)从这个班中任取1人,其数学成绩达到或超过年级文科平均分的概率是0.66. 分析 求出此班在[100,110),[110,120),[120,130),[130,140),[140,150)分数段的共有33人,根据概率公式计算即可
解答 解:[80,90)人数为0.08×10×50=4,
[90,100)人数为0.026×10×50=13,
[100,110)人数为0.038×10×50=19,
[110,120)人数为0.014×10×50=7,
[130,140)人数为0.004×10×50=2,
其中[120,130)人数为50-(4+13+19+7+2)=5,
此班在[100,110),[110,120),[120,130),[130,140),[140,150)分数段的共有19+7+2+5=33,
所求概率P=$\frac{33}{50}$=0.66,
故答案为:0.66.
点评 本题考查了频率分布直方图,考查了古典概型的概率计算,解题的关键是读懂频率分布直方图的数据.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{π}$ | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | C是B的真子集、B是A的真子集 | B. | A是B的真子集、B是C的真子集 | ||
| C. | C是A的真子集、A=B | D. | A=B=C |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com