练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．下列函数中是奇函数的是（　　）
    A．y=-|sinx|B．y=sin（-|x|）C．y=sin|x|D．y=xsin|x|

    分析 根据函数奇偶性的定义进行判断即可．

    解答 解：A．f（-x）=-|sin（-x）|=-|sinx|=f（x），则函数f（x）为偶函数，
    B．f（-x）=sin（-|-x|）|=sin（-|x|）=f（x），则函数f（x）为偶函数，
    C．f（-x）=sin（|-x|）|=sin（|x|）=f（x），则函数f（x）为偶函数，
    D．f（-x）=-xsin（|-x|）|=-xsin（|x|）=-f（x），则函数f（x）为奇函数，
    故选：D．

    点评 本题主要考查函数的奇偶性的判断，根据函数奇偶性的定义是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    13．已知M是椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1上一点，焦点为F1，F2，则△MF1F2的周长是16．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

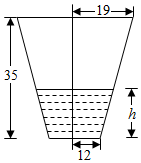    14．降水量是指水平地面上单位面积的降水的深度，用上口直径为38cm，底面直径为24cm，深为35cm的圆台形水桶（轴截面如图）来测量降水量，如果在一次降雨过程中，用此桶盛得的雨水正好是桶深的$\frac{1}{7}$，求这次降雨的降水量（精确到1mm）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．设各项均为正数的数列{an}的前n项和为Sn，且存在正数t，使对所有的正整数n，都有$\sqrt{t{S}_{n}}$=$\frac{t+{a}_{n}}{2}$成立．
    （1）求数列{an}的通项公式；
    （2）如果$\frac{\sqrt{{S}_{n}}}{{a}_{n}}$＜t对一切n∈N*恒成立，求t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．设非零向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{c}$|，$\overrightarrow{a}$+$\overrightarrow{b}$=$\sqrt{3}$$\overrightarrow{c}$，则向量$\overrightarrow{a}$与向量$\overrightarrow{c}$的夹角为（　　）
    A．150°B．120°C．60°D．30°

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．角的顶点与坐标原点重合，角的始边与x轴的非负半轴重合，则角α与角180°+α的终边关系为（　　）
    A．一定关于x轴对称B．一定关于y轴对称C．关于原点对称D．不具有对称性

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知sinα+cosα=$\frac{\sqrt{2}}{3}$，α∈（0，π）．
    （1）求$\frac{sin2α+2si{n}^{2}α}{1-tanα}$的值；
    （2）若cosβ+sinβ=-$\frac{\sqrt{2}}{3}$，β∈（0，π），求角α+β的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知数列{an}，{bn}，其中a1=l，an=$\frac{1}{b_n}+\frac{1}{2}$，$\frac{4}{{{b_{n+1}}{b_n}}}=\frac{6}{{{b_{n+1}}}}-\frac{3}{b_n}$，（n∈N* ）
    （1）求证：数列{bn-$\frac{4}{3}$}是等比数列；
    （2）求数列{bn}的通项公式及数列{anbn}的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．某食品厂为了检查一条自动包装流水线的生产情况，随即抽取该流水线上40件产品作为样本算出他们的重量（单位：克）重量的分组区间为（490，495]，（495，500]，…（510，515]，由此得到样本的频率分布直方图，如图所示．
    （1）根据频率分布直方图，求重量不超过500克的产品数量；
    （2）在上述抽取的40件产品中任取2件，设Y为重量不超过500克的产品数量，求Y的分布列及期望；
    （3）从流水线上任取5件产品，求恰有2件产品合格的重量不超过500克的概率．

    查看答案和解析>>

    同步练习册答案