
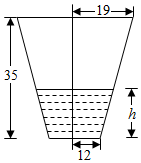
 降水量是指水平地面上单位面积的降水的深度,用上口直径为38cm,底面直径为24cm,深为35cm的圆台形水桶(轴截面如图)来测量降水量,如果在一次降雨过程中,用此桶盛得的雨水正好是桶深的$\frac{1}{7}$,求这次降雨的降水量(精确到1mm).
降水量是指水平地面上单位面积的降水的深度,用上口直径为38cm,底面直径为24cm,深为35cm的圆台形水桶(轴截面如图)来测量降水量,如果在一次降雨过程中,用此桶盛得的雨水正好是桶深的$\frac{1}{7}$,求这次降雨的降水量(精确到1mm). 分析 因为桶中的水可以看作一个圆台,圆台的体积就是降雨量,而圆台的下底面与水桶下底面相同,上底面是与水桶上下底面平行的截面,所以只需求出水桶截面圆直径即可,利用水桶的上下底面,截面平行,可得一些成比例线段,根据上下底面直径,可求出截面圆直径,再利用圆台的体积公式就可求出降雨量.
解答 解:如图所示,
水的高度O1O2=$\frac{1}{7}$×35=5cm,
又$\frac{{{A}_{1}B}_{1}}{{{A}_{2}B}_{1}}$=$\frac{AB}{{A}_{2}B}$,即$\frac{{{A}_{1}B}_{1}}{5}$=$\frac{7}{35}$,
所以A1B1=1,所以水面半径O1A1=12+1=13cm;
故雨水的体积为V=$\frac{1}{3}$πh(${{r}_{1}}^{2}$+r1r2+${{r}_{2}}^{2}$)=$\frac{1}{3}$π•5•(122+12•13+132)=$\frac{2345π}{3}$cm3
水桶上口面面积S=π•192=361πcm2
每平方厘米的降雨量h=$\frac{\frac{2345π}{3}}{361π}$≈2.2(cm),
所以降雨量约为22mm.
点评 本题考查了应用圆台体积公式求几何体体积的应用问题,也考查了计算能力的应用问题,是基础题目.


科目:高中数学 来源: 题型:选择题
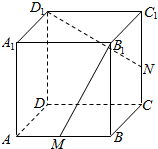 如图所示,在正方体ABCD-A1B1C1D1中,M,N分别是线段AB,CC1的中点,∨MB1P的顶点P在棱CC1与棱C1D1上运动,有以下四个命题:
如图所示,在正方体ABCD-A1B1C1D1中,M,N分别是线段AB,CC1的中点,∨MB1P的顶点P在棱CC1与棱C1D1上运动,有以下四个命题:| A. | ① | B. | ①③ | C. | ②③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0] | B. | [$-\frac{2}{3}$,$\frac{2}{3}$] | C. | (-∞,-$\frac{2}{3}$] | D. | (-∞,-$\frac{2}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com