
分析 由bn=$\sqrt{1+4{a}_{n}}$>0(n∈N),可得b1=3,${b}_{n}^{2}$=1+4an,代入8an+1=2an+$\sqrt{1+4{a}_{n}}$-1(n∈N),可得:2bn+1=bn+1,变形为:bn+1-1=$\frac{1}{2}({b}_{n}-1)$,利用等比数列的通项公式可得:bn.可得cn=$\frac{n}{{2}^{n}}$.再利用“错位相减法”与等比数列的前n项和公式即可得出.
解答 证明:∵bn=$\sqrt{1+4{a}_{n}}$>0(n∈N),
∴b1=3,${b}_{n}^{2}$=1+4an,
代入8an+1=2an+$\sqrt{1+4{a}_{n}}$-1(n∈N),
∴$8×\frac{{b}_{n+1}^{2}-1}{4}$=2×$\frac{{b}_{n}^{2}-1}{4}$+bn-1,
化为$(2{b}_{n+1})^{2}$=$({b}_{n}+1)^{2}$,
可得:2bn+1=bn+1,
变形为:bn+1-1=$\frac{1}{2}({b}_{n}-1)$,
∴数列{bn-1}是等比数列,首项为2,公比为$\frac{1}{2}$.
∴bn-1=2×$(\frac{1}{2})^{n-1}$=22-n.
∴数列cn=$\frac{n({b}_{n}-1)}{4}$=$\frac{n}{4}×{2}^{2-n}$=$\frac{n}{{2}^{n}}$.
∴数列{cn}的前n项和为Sn=$\frac{1}{2}$+$\frac{2}{{2}^{2}}+\frac{3}{{2}^{3}}$+…+$\frac{n}{{2}^{n}}$,
$\frac{1}{2}{S}_{n}$=$\frac{1}{{2}^{2}}$+$\frac{2}{{2}^{3}}$+…+$\frac{n-1}{{2}^{n}}$+$\frac{n}{{2}^{n+1}}$,
∴$\frac{1}{2}{S}_{n}$=$\frac{1}{2}+\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n}}$-$\frac{n}{{2}^{n+1}}$=$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$-$\frac{n}{{2}^{n+1}}$=1-$\frac{2+n}{{2}^{n+1}}$,
∴Sn=2-$\frac{2+n}{{2}^{n}}$<2.
点评 本题考查了递推关系、等比数列的通项公式及其前n项和公式、“错位相减法”,考查了推理能力与计算能力,属于中档题.


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:选择题
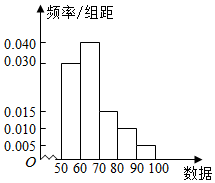
| A. | 63、64、66 | B. | 65、65、67 | C. | 65、64、66 | D. | 64、65、64 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
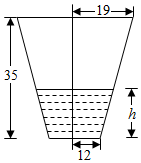 降水量是指水平地面上单位面积的降水的深度,用上口直径为38cm,底面直径为24cm,深为35cm的圆台形水桶(轴截面如图)来测量降水量,如果在一次降雨过程中,用此桶盛得的雨水正好是桶深的$\frac{1}{7}$,求这次降雨的降水量(精确到1mm).
降水量是指水平地面上单位面积的降水的深度,用上口直径为38cm,底面直径为24cm,深为35cm的圆台形水桶(轴截面如图)来测量降水量,如果在一次降雨过程中,用此桶盛得的雨水正好是桶深的$\frac{1}{7}$,求这次降雨的降水量(精确到1mm).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com