
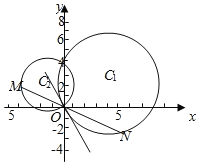
【题目】已知圆![]() 与y轴交于O,A两点,圆C2过O,A两点,且直线C2O与圆C1相切;
与y轴交于O,A两点,圆C2过O,A两点,且直线C2O与圆C1相切;
(1)求圆C2的方程;
(2)若圆C2上一动点M,直线MO与圆C1的另一交点为N,在平面内是否存在定点P使得PM=PN始终成立,若存在求出定点坐标,若不存在,说明理由.
【答案】(1)![]() ;(2)存在,且为
;(2)存在,且为![]() .
.
【解析】试题分析:(1)由(x﹣4)2+(y﹣2)2=20,令x=0,解得y=0或4.圆C2过0,A两点,可设圆C2的圆心C1(a,2).直线C2O的方程为:y=![]() x,即x﹣2y=0.利用直线C20与圆C1相切的性质即可得出;(2)存在,且为P(3,4).设直线OM的方程为:y=kx.代入圆C2的方程可得:(1+k2)x2+(2﹣4k)x=0.可得M的坐标.同理可得N的坐标.设P(x,y),线段MN的中点E,利用kPEk=﹣1即可得出.
x,即x﹣2y=0.利用直线C20与圆C1相切的性质即可得出;(2)存在,且为P(3,4).设直线OM的方程为:y=kx.代入圆C2的方程可得:(1+k2)x2+(2﹣4k)x=0.可得M的坐标.同理可得N的坐标.设P(x,y),线段MN的中点E,利用kPEk=﹣1即可得出.
详解:
(1)由(x﹣4)2+(y﹣2)2=20,令x=0,解得y=0或4.
∵圆C2过O,A两点,∴可设圆C2的圆心C1(a,2).
直线C2O的方程为:y=![]() x,即x﹣2y=0.
x,即x﹣2y=0.
∵直线C2O与圆C1相切,∴![]() =
=![]() ,解得a=﹣1,
,解得a=﹣1,
∴圆C2的方程为:(x+1)2+(y﹣2)2=![]() ,化为:x2+y2+2x﹣4y=0.
,化为:x2+y2+2x﹣4y=0.
(2)存在,且为P(3,4).
设直线OM的方程为:y=kx.
代入圆C2的方程可得:(1+k2)x2+(2﹣4k)x=0.
xM=![]() ,yM=
,yM=![]() .
.
代入圆C1的方程可得:(1+k2)x2﹣(8+4k)x=0.
xN=![]() ,yN=
,yN=![]() .
.
设P(x,y),线段MN的中点E![]() .
.
则 ×k=﹣1,
×k=﹣1,
化为:k(4﹣y)+(3﹣x)=0,
令4﹣y=3﹣x=0,解得x=3,y=4.
∴P(3,4)与k无关系.
∴在平面内是存在定点P(3,4)使得PM=PN始终成立.


科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图像是由函数
的图像是由函数![]() 的图像经如下变换得到:先将
的图像经如下变换得到:先将![]() 图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移
图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移![]() 个单位长度.
个单位长度.
(Ⅰ)求函数![]() 的解析式,并求其图像的对称轴方程;
的解析式,并求其图像的对称轴方程;
(Ⅱ)已知关于![]() 的方程
的方程![]() 在
在![]() 内有两个不同的解
内有两个不同的解![]() .
.
(1)求实数m的取值范围;
(2)证明:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点![]() 为圆心的圆过点
为圆心的圆过点![]() 和
和![]() ,线段
,线段![]() 的垂直平分线交圆
的垂直平分线交圆![]() 于点
于点![]() 、
、![]() ,且
,且![]() ,
,
(1)求直线![]() 的方程; (2)求圆
的方程; (2)求圆![]() 的方程。
的方程。
(3)设点![]() 在圆
在圆![]() 上,试探究使
上,试探究使![]() 的面积为 8 的点
的面积为 8 的点![]() 共有几个?证明你的结论
共有几个?证明你的结论
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组: ![]()
![]() ,并整理得到如下频率分布直方图:
,并整理得到如下频率分布直方图: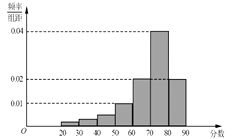
(Ⅰ)从总体的400名学生中随机抽取一人,估计其分数小于70的概率;
(Ⅱ)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(Ⅲ)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
查看答案和解析>>
科目:高中数学 来源: 题型:
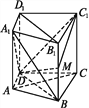
【题目】如图,在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.
(1)求证:B1D1∥平面A1BD;
(2)求证:MD⊥AC;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学调查了某班全部 45 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
参加书法社团 | 未参加书法社团 | |
参加演讲社团 | 8 | 5 |
未参加书法社团 | 2 | 30 |
(1)从该班随机选 1 名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的 8 名同学中,有 5 名男同学![]() ,3名女同学
,3名女同学![]() .现从这 5 名男同学和 3 名女同学中各随机选 1 人,求
.现从这 5 名男同学和 3 名女同学中各随机选 1 人,求![]() 被选中且
被选中且![]() 未被选中的概率.
未被选中的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com