
【题目】今年的国庆假期是实施免收小型客车高速通行费后的第一个重大节假日,有一个群名为“天狼星”的自驾游车队.该车队是由31辆车身长都约为5m(以5m计算)的同一车型组成的,行程中经过一个长为2725m的隧道(通过该隧道的车速不能超过25m/s),匀
速通过该隧道,设车队的速度为xm/s,根据安全和车流的需要,当0<x≤12时,相邻两车之间保持20m的距离;当12<x≤25时,相邻两车之间保持( ![]() )m的距离.自第1辆车车头进入隧道至第31辆车车尾离开隧道所用的时间为y(s).
)m的距离.自第1辆车车头进入隧道至第31辆车车尾离开隧道所用的时间为y(s).
(1)将y表示为x的函数;
(2)求该车队通过隧道时间y的最小值及此时车队的速度.
【答案】
(1)解:∵当0<x≤12时,相邻两车之间保持20m的距离;
当12<x≤25时,相邻两车之间保持( ![]() )m的距离,
)m的距离,
∴当0<x≤12时,y= ![]() =
= ![]() ;
;
当12<x≤25时,y= ![]() =5x+
=5x+ ![]() +10
+10
∴y= 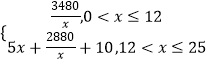
(2)解:当0<x≤12时,y= ![]() ,∴x=12m/s时,ymin=290s;
,∴x=12m/s时,ymin=290s;
当12<x≤25时,y=5x+ ![]() +10≥2
+10≥2 ![]() +10=250s
+10=250s
当且仅当5x= ![]() ,即x=24m/s时取等号,即x=24m/s时,ymin=250s
,即x=24m/s时取等号,即x=24m/s时,ymin=250s
∵290>250,∴x=24m/s时,ymin=250s.
答:该车队通过隧道时间y的最小值为250s及此时该车队的速度为24m/s
【解析】(1)利用当0<x≤12时,相邻两车之间保持20m的距离;当12<x≤25时,相邻两车之间保持( ![]() )m的距离,可得分段函数;(2)分段求出函数的最小值,即可得到分段函数的最小值.
)m的距离,可得分段函数;(2)分段求出函数的最小值,即可得到分段函数的最小值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点. 
(1)证明:MN∥平面PAB;
(2)求直线AN与平面PMN所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为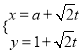 (
(![]() 为参数,
为参数, ![]() ),以
),以![]() 为极点,
为极点, ![]() 轴非负半轴为极轴,建立极坐标系,曲线
轴非负半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知曲线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ()的焦距为4,左、右焦点分别为
()的焦距为4,左、右焦点分别为![]() ,且
,且![]() 与抛物线
与抛物线![]() :
: ![]()
![]() 的交点所在的直线经过
的交点所在的直线经过![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过![]()
![]() 的直线
的直线![]()
![]() 与
与![]() 交于
交于![]() 两点,与抛物线
两点,与抛物线![]() 无公共点,求
无公共点,求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() (x>0),数列{an}满足
(x>0),数列{an}满足 ![]() (n∈N* , 且n≥2).
(n∈N* , 且n≥2).
(1)求数列{an}的通项公式;
(2)设Tn=a1a2﹣a2a3+a3a4﹣a4a5+…+(﹣1)n﹣1anan+1 , 若Tn≥tn2对n∈N*恒成立,求实数t的取值范围;
(3)是否存在以a1为首项,公比为q(0<q<5,q∈N*)的数列{a ![]() },k∈N* , 使得数列{a
},k∈N* , 使得数列{a ![]() }中每一项都是数列{an}中不同的项,若存在,求出所有满足条件的数列{nk}的通项公式;若不存在,说明理由.
}中每一项都是数列{an}中不同的项,若存在,求出所有满足条件的数列{nk}的通项公式;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面四组函数中,f(x)与g(x)表示同一个函数的是( )
A.f(x)=|x|, ![]()
B.f(x)=2x, ![]()
C.f(x)=x, ![]()
D.f(x)=x, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位共有10名员工,他们某年的收入如下表:
员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
年薪(万元) | 4 | 4.5 | 6 | 5 | 6.5 | 7.5 | 8 | 8.5 | 9 | 51 |
(1)求该单位员工当年年薪的平均值和中位数;
(2)从该单位中任取2人,此2人中年薪收入高于7万的人数记为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
(3)已知员工年薪收入与工作年限成正相关关系,某员工工作第一年至第四年的年薪分别为4万元,5.5万元,6万元,8.5万元,预测该员工第五年的年薪为多少?
附:线性回归方程![]() 中系数计算公式分别为:
中系数计算公式分别为:
 ,
, ![]() ,其中
,其中![]() 为样本均值.
为样本均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE. 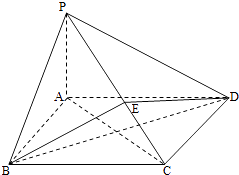
(1)证明:BD⊥平面PAC;
(2)若PA=1,AD=2,求二面角B﹣PC﹣A的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com