
【题目】设函数f(x)= ![]() (x>0),数列{an}满足
(x>0),数列{an}满足 ![]() (n∈N* , 且n≥2).
(n∈N* , 且n≥2).
(1)求数列{an}的通项公式;
(2)设Tn=a1a2﹣a2a3+a3a4﹣a4a5+…+(﹣1)n﹣1anan+1 , 若Tn≥tn2对n∈N*恒成立,求实数t的取值范围;
(3)是否存在以a1为首项,公比为q(0<q<5,q∈N*)的数列{a ![]() },k∈N* , 使得数列{a
},k∈N* , 使得数列{a ![]() }中每一项都是数列{an}中不同的项,若存在,求出所有满足条件的数列{nk}的通项公式;若不存在,说明理由.
}中每一项都是数列{an}中不同的项,若存在,求出所有满足条件的数列{nk}的通项公式;若不存在,说明理由.
【答案】
(1)解:因为 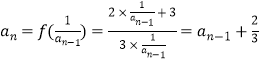 ,(n∈N*,且n≥2),
,(n∈N*,且n≥2),
所以an﹣an﹣1= ![]() .
.
因为a1=1,
所以数列{an}是以1为首项,公差为 ![]() 的等差数列.
的等差数列.
所以an= ![]()
(2)解:①当n=2m,m∈N*时,Tn=T2m=a1a2﹣a2a3+a3a4﹣a4a5++(﹣1)2m﹣1a2ma2m+1=a2(a1﹣a3)+a4(a3﹣a5)++a2m(a2m﹣1﹣a2m+1)=﹣ ![]() =﹣
=﹣ ![]() =﹣
=﹣ ![]() .
.
②当n=2m﹣1,m∈N*时,Tn=T2m﹣1=T2m﹣(﹣1)2m﹣1a2ma2m+1=﹣ ![]() =
= ![]() .
.
所以Tn= 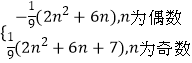
要使Tn≥tn2对n∈N*恒成立,
只要使﹣ ![]() ,(n为偶数)恒成立.
,(n为偶数)恒成立.
只要使﹣ ![]() ,对n为偶数恒成立,
,对n为偶数恒成立,
故实数t的取值范围为 ![]()
(3)解:由an= ![]() ,知数列{an}中每一项都不可能是偶数.
,知数列{an}中每一项都不可能是偶数.
①如存在以a1为首项,公比q为2或4的数列{ank},k∈N*,
此时{ank}中每一项除第一项外都是偶数,故不存在以a1为首项,公比为偶数的数列{ank}.
②当q=1时,显然不存在这样的数列{ank}.
当q=3时,若存在以a1为首项,公比为3的数列{ank},k∈N*.
则 ![]() =1,n1=1,
=1,n1=1, ![]() =
= ![]() ,nk=
,nk= ![]() .
.
所以满足条件的数列{nk}的通项公式为nk= ![]()
【解析】(1)由 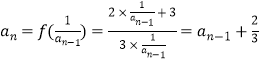 ,(n∈N* , 且n≥2),知
,(n∈N* , 且n≥2),知 ![]() .再由a1=1,能求出数列{an}的通项公式;(2)当n=2m,m∈N*时,Tn=T2m=a1a2﹣a2a3+a3a4﹣a4a5++(﹣1)2m﹣1a2ma2m+1=a2(a1﹣a3)+a4(a3﹣a5)++a2m(a2m﹣1﹣a2m+1)=
.再由a1=1,能求出数列{an}的通项公式;(2)当n=2m,m∈N*时,Tn=T2m=a1a2﹣a2a3+a3a4﹣a4a5++(﹣1)2m﹣1a2ma2m+1=a2(a1﹣a3)+a4(a3﹣a5)++a2m(a2m﹣1﹣a2m+1)= ![]() =
= ![]() =
= ![]() .当n=2m﹣1,m∈N*时,Tn=T2m﹣1=T2m﹣(﹣1)2m﹣1a2ma2m+1=
.当n=2m﹣1,m∈N*时,Tn=T2m﹣1=T2m﹣(﹣1)2m﹣1a2ma2m+1= ![]() =
= ![]() .由此入手能求出实数t的取值范围.(3)由
.由此入手能求出实数t的取值范围.(3)由 ![]() ,知数列{an}中每一项都不可能是偶数.如存在以a1为首项,公比q为2或4的数列{ank},k∈N* , 此时{ank}中每一项除第一项外都是偶数,故不存在以a1为首项,公比为偶数的数列{ank}.当q=1时,显然不存在这样的数列{ank}.当q=3时,
,知数列{an}中每一项都不可能是偶数.如存在以a1为首项,公比q为2或4的数列{ank},k∈N* , 此时{ank}中每一项除第一项外都是偶数,故不存在以a1为首项,公比为偶数的数列{ank}.当q=1时,显然不存在这样的数列{ank}.当q=3时, ![]() ,n1=1,
,n1=1, ![]() ,
, ![]() .所以满足条件的数列{nk}的通项公式为
.所以满足条件的数列{nk}的通项公式为 ![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC—A1B1C1中,AB=BC=BB1, ![]() ,D为AC上的点,B1C∥平面A1BD;
,D为AC上的点,B1C∥平面A1BD;
(1)求证:BD⊥平面![]() ;
;
(2)若![]() 且
且![]() ,求三棱锥A-BCB1的体积.
,求三棱锥A-BCB1的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣4x﹣5≥0},集合B={x|2a≤x≤a+2}.
(1)若a=﹣1,求A∩B和A∪B;
(2)若A∩B=B,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今年的国庆假期是实施免收小型客车高速通行费后的第一个重大节假日,有一个群名为“天狼星”的自驾游车队.该车队是由31辆车身长都约为5m(以5m计算)的同一车型组成的,行程中经过一个长为2725m的隧道(通过该隧道的车速不能超过25m/s),匀
速通过该隧道,设车队的速度为xm/s,根据安全和车流的需要,当0<x≤12时,相邻两车之间保持20m的距离;当12<x≤25时,相邻两车之间保持( ![]() )m的距离.自第1辆车车头进入隧道至第31辆车车尾离开隧道所用的时间为y(s).
)m的距离.自第1辆车车头进入隧道至第31辆车车尾离开隧道所用的时间为y(s).
(1)将y表示为x的函数;
(2)求该车队通过隧道时间y的最小值及此时车队的速度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=ax2﹣2ax+b+1(a>0)在区间[2,3]上有最大值4,最小值1.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)设g(x)= ![]() .若不等式g(2x)﹣k2x≥0对任意x∈[1,2]恒成立,求k的取值范围.
.若不等式g(2x)﹣k2x≥0对任意x∈[1,2]恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F为抛物线y2=x的焦点,点A,B在该抛物线上且位于x轴的两侧, ![]()
![]() =2(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是( )
=2(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是( )
A.2
B.3
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种多面体玩具共有12个面,在其十二个面上分别标有数字1,2,3,…,12.若该玩具质地均匀,则抛掷该玩具后,任何一个数字所在的面朝上的概率均相等.
为检验某批玩具是否合格,制定检验标准为:多次抛掷该玩具,并记录朝上的面上标记的数字,若各数字出现的频率的极差不超过0.05.则认为该玩具合格.

(1)对某批玩具中随机抽取20件进行检验,将每个玩具各面数字出现频率的极差绘制成茎叶图(如图所示),试估计这批玩具的合格率;
(2)现有该种类玩具一个,将其抛掷100次,并记录朝上的一面标记的数字,得到如下数据:
朝上面的数字 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
次数 | 9 | 7 | 8 | 6 | 10 | 9 | 9 | 8 | 10 | 9 | 7 | 8 |
1)试判定该玩具是否合格;
2)将该玩具抛掷一次,记事件![]() :向上的面标记数字是完全平方数(能写成整数的平方形式的数,如
:向上的面标记数字是完全平方数(能写成整数的平方形式的数,如![]() ,9为完全平方数);事件
,9为完全平方数);事件![]() :向上的面标记的数字不超过4.试根据上表中的数据,完成以下列联表(其中
:向上的面标记的数字不超过4.试根据上表中的数据,完成以下列联表(其中![]() 表示
表示![]() 的对立事件),并回答在犯错误的概率不超过0.01的前提下,能否认为事件
的对立事件),并回答在犯错误的概率不超过0.01的前提下,能否认为事件![]() 与事件
与事件![]() 有关.
有关.
|
| 合计 | |
| |||
| |||
合计 | 100 |
(参考公式及数据: 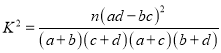 ,
, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com