
如图,直角梯形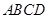 中,
中,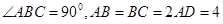 ,点
,点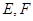 分别是
分别是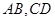 的中点,点
的中点,点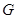 在
在 上,沿
上,沿 将梯形
将梯形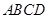 翻折,使平面
翻折,使平面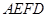
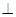 平面
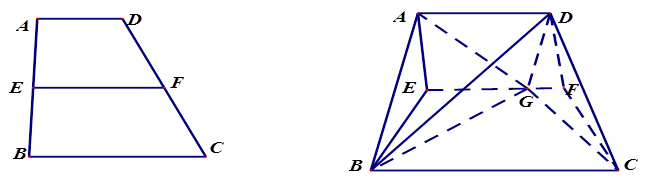
平面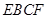 .
.
(1)当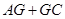 最小时,求证:
最小时,求证: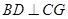 ;
;
(2)当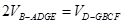 时,求二面角
时,求二面角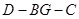 平面角的余弦值.
平面角的余弦值.
(1)参考解析;(2)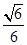
解析试题分析:(1)因为当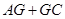 最小时,及连结AC与EF的交点即为G点,通过三角形的相似可得到EG的长度.需要证明直线与直线垂直,根据题意建立空间直角坐标系,即可得到相关各点的坐标,从而写出相关向量,即可判断直线的垂直关系.
最小时,及连结AC与EF的交点即为G点,通过三角形的相似可得到EG的长度.需要证明直线与直线垂直,根据题意建立空间直角坐标系,即可得到相关各点的坐标,从而写出相关向量,即可判断直线的垂直关系.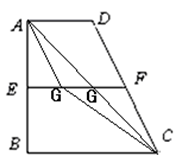
(2)由题意所给的体积关系可确定点G的位置,求二面角关键是转化为两平面的法向量的夹角,由于平面BCG的法向量易得,关键是求出平面DGB的法向量.通过待定系数法即可求得,还需判断二面角与法向量夹角的大小关系.解法二用到的推理论证的数学思想很重要.
试题解析:(1)证明:∵点 、
、 分别是
分别是 、
、 的中点,∴EF//BC
的中点,∴EF//BC
又∠ABC=90°∴AE⊥EF,∵平面AEFD⊥平面EBCF,
∴AE⊥平面EBCF,AE⊥EF,AE⊥BE, 又BE⊥EF,
如图建立空间坐标系E﹣xyz.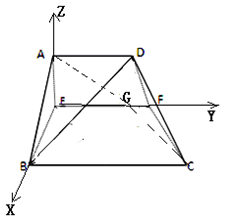
翻折前,连结AC交EF于点G,此时点G使得AG+GC最小.
EG=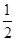 BC=2,又∵EA=EB=2.
BC=2,又∵EA=EB=2.
则A(0,0,2),B(2,0,0),C(2,4,0), D(0,2,2),E(0,0,0),G(0,2,0),
∴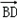 =(﹣2,2,2),
=(﹣2,2,2),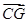 =(-2,-2,0)
=(-2,-2,0)
∴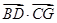 =(﹣2,2,2)(-2,-2,0)=0,
=(﹣2,2,2)(-2,-2,0)=0,
∴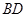 ⊥
⊥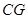
(2)解法一:设EG=k,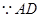 ∥平面
∥平面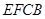 ,
,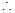 点D到平面EFCB的距离为即为点A到平面EFCB的距离.
点D到平面EFCB的距离为即为点A到平面EFCB的距离.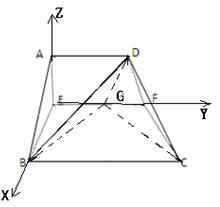
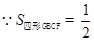 [(3- k)+4]×2=7-k
[(3- k)+4]×2=7-k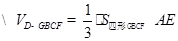 =
=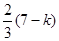
又 =
=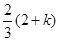 ,
,
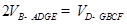 ,
,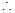
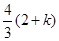 =
=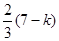 ,
,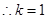 即EG=1
即EG=1
设平面DBG的法向量为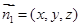 ,∵G(0,1,0),
,∵G(0,1,0),
∴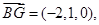
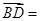 (-2,2,2),
(-2,2,2),
则 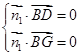 ,即
,即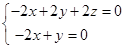
取x=1,则y=2,z=-1,∴
面BCG的一个法向量为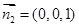
则cos<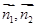 >=
>=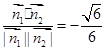 由于所求二面角D-BF-C的平面角为锐角,
由于所求二面角D-BF-C的平面角为锐角,
所以此二面角平面角的余弦值为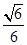
(2)解法二:由解法一得EG=1,过点D作DH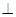 EF,垂足H,过点H作BG延长线的垂线垂足O,连接OD.
EF,垂足H,过点H作BG延长线的垂线垂足O,连接OD. 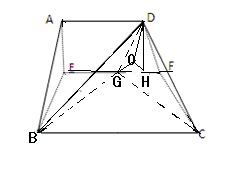
∵平面AEFD⊥平面EBCF, DH
DH 平面EBCF,
平面EBCF, OD
OD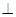 OB,所以
OB,所以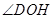 就是所求的二面角
就是所求的二面角 的平面角.由于HG=1,在
的平面角.由于HG=1,在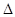 OHG中
OHG中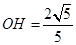 ,
,
又DH=2,在 DOH中
DOH中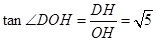
所以此二面角平面角的余弦值为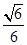
考点:1.图形的翻折问题.2.线面垂直的判定.3.二面角的求法.4.空间坐标系中的运算.5.空间想象能力.


科目:高中数学 来源: 题型:解答题
如图,直三棱柱ABC-A1B1C1中,AB⊥AC,D、E分别为AA1、B1C的中点,DE⊥平面BCC1
(1)证明:AB=AC
(2)设二面角A-BD-C为60°,求B1C与平面BCD所成的角的大小
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,在四棱锥P-ABCD中,PC⊥平面ABCD,PC=2,在四边形ABCD中,∠B=∠C=90°,AB=4,CD=1,点M在PB上,PB=4PM,PB与平面ABCD成30°的角.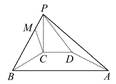
求证:(1)CM∥平面PAD.
(2)平面PAB⊥平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在四棱锥O—ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA中点。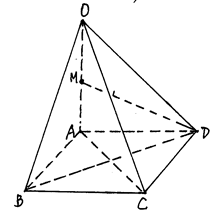
(1)求证:直线BD⊥平面OAC;
(2)求直线MD与平面OAC所成角的大小;
(3)求点A到平面OBD的距离。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知直三棱柱ABC-A1B1C1中,AC⊥BC,D为AB的中点,AC=BC=BB1.
求证:(1)BC1⊥AB1.
(2)BC1∥平面CA1D.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图1,A,D分别是矩形A1BCD1上的点,AB=2AA1=2AD=2,DC=2DD1,把四边形A1ADD1沿AD折叠,使其与平面ABCD垂直,如图2所示,连接A1B,D1C得几何体ABA1DCD1.
(1)当点E在棱AB上移动时,证明:D1E⊥A1D;
(2)在棱AB上是否存在点E,使二面角D1ECD的平面角为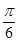 ?若存在,求出AE的长;若不存在,请说明理由.
?若存在,求出AE的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在直三棱柱ABCA1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,A1A= ,M是CC1的中点.
,M是CC1的中点.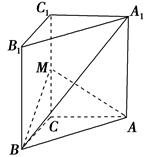
(1)求证:A1B⊥AM;
(2)求二面角BAMC的平面角的大小..
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com