
如图,在四棱锥O—ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA中点。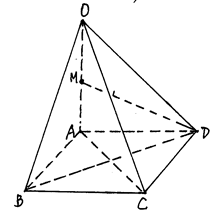
(1)求证:直线BD⊥平面OAC;
(2)求直线MD与平面OAC所成角的大小;
(3)求点A到平面OBD的距离。
(1)详见解析;(2)30°;(3)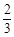 .
.
解析试题分析:方法一:向量法以A为原点,AB,AD,AO分别x轴,y轴,z轴建立空间直角坐标系,A-xyz (1)利用向量的数量积的坐标运算与垂直的关系,∵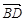 =(-1,1,0),
=(-1,1,0),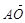 =(0,0,2),
=(0,0,2), =(1,1,0)∴
=(1,1,0)∴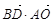 =0,
=0,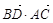 =-1+1=0∴BD⊥AD,BD⊥AC,又AO∩AC=A故BD⊥平面OAC ;
=-1+1=0∴BD⊥AD,BD⊥AC,又AO∩AC=A故BD⊥平面OAC ;
(2)取平面OAC的法向量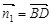 =(-1,1,0),又
=(-1,1,0),又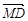 =(0,1,-1)[ K则:
=(0,1,-1)[ K则: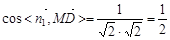
∴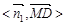 =60°故:MD与平面OAC所成角为30°;
=60°故:MD与平面OAC所成角为30°;
(3)设平面OBD的法向量为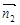 =(x,y,z),则
=(x,y,z),则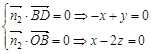
取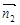 =(2,2,1)则点A到平面OBD的距离为d=
=(2,2,1)则点A到平面OBD的距离为d=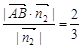 ;
;
方法二:几何法(1)由线面垂直的的判断定理证明,由OA⊥底面ABCD,OA⊥BD,∵底面ABCD是边长为1的正方形∴BD⊥AC ∴BD⊥平面OAC ;(2)先构造线面所成的角,设AC与BD交于点E,连结EM,则∠DME是直线MD与平面OAC折成的角,又由于∵MD=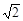 ,DE=
,DE=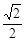 ∴直线MD与平面OAC折成的角为30°;(3)构造点到面的距离,作AH⊥OE于点H,∵BD⊥平面OAC∴BO⊥AH
∴直线MD与平面OAC折成的角为30°;(3)构造点到面的距离,作AH⊥OE于点H,∵BD⊥平面OAC∴BO⊥AH
线段AH的长就是点A到平面OBD的距离,有AH=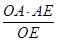 可知点A到平面OBD的距离为
可知点A到平面OBD的距离为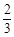 .
.
试题解析:方法一:以A为原点,AB,AD,AO分别x轴,y轴,z轴建立空间直角坐标系,A-xyz。
(1)∵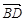 =(-1,1,0),
=(-1,1,0),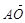 =(0,0,2),
=(0,0,2), =(1,1,0)
=(1,1,0)
∴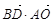 =0,
=0,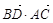 =-1+1=0
=-1+1=0
∴BD⊥AD,BD⊥AC,又AO∩AC=A
故BD⊥平面OAC 4分
(2)取平面OAC的法向量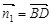 =(-1,1,0),又
=(-1,1,0),又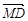 =(0,1,-1)[来源:学科网ZXXK]
=(0,1,-1)[来源:学科网ZXXK]
则: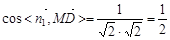
∴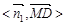 =60°
=60°
故:MD与平面OAC所成角为30° 8分
(3)设平面OBD的法向量为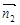 =(x,y,z),则
=(x,y,z),则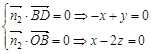
取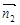 =(2,2,1)
=(2,2,1)
则点A到平面OBD的距离为d=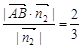 12分
12分
方法二:(1)由OA⊥底面ABCD,OA⊥BD。
∵底面ABCD是边长为1的正方形
∴BD⊥AC ∴BD⊥平面OAC 4分
(2)设AC与BD交于点E,连结EM,则∠DME是直线MD与平面OAC折成的角
∵MD=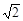 ,DE=
,DE=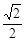
∴直线MD与平面OAC折成的角为30° 8分
(3)作AH⊥OE于点H。
∵BD⊥平面OAC
∴BO⊥AH
线段AH的长就是点A到平面OBD的距离。
∴AH=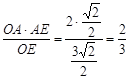
∴点A到平面OBD的距离为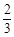 12分
12分
考点:1.线面垂直的的判断定理;2.线面成角.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:解答题
如图, 已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且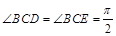 ,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.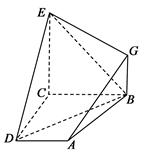
(1)求证:AG 平面BDE;
平面BDE;
(2)求:二面角G DE
DE B的余弦值.
B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,在多面体ABCD-A1B1C1D1中,上、下两个底面A1B1C1D1和ABCD互相平行,且都是正方形,DD1⊥底面ABCD,AB∥A1B1,AB=2A1B1=2DD1=2a.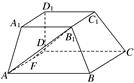
(1)求异面直线AB1与DD1所成角的余弦值;
(2)已知F是AD的中点,求证:FB1⊥平面BCC1B1.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,在多面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,BA⊥AC,ED⊥DG,EF∥DG,且AC=1,AB=ED=EF=2,AD=DG=4.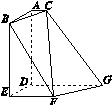
(1)求证:BE⊥平面DEFG;
(2)求证:BF∥平面ACGD;
(3)求二面角F-BC-A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在等腰梯形ABCD中,AD∥BC,AD=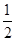 BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).
BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).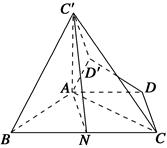
(1)求证:AC⊥平面ABC′;
(2)求证:C′N∥平面ADD′;
(3)求二面角A-C′N-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在三棱锥SABC中,底面是边长为2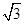 的正三角形,点S在底面ABC上的射影O恰是AC的中点,侧棱SB和底面成45°角.
的正三角形,点S在底面ABC上的射影O恰是AC的中点,侧棱SB和底面成45°角.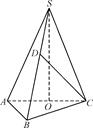
(1)若D为侧棱SB上一点,当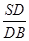 为何值时,CD⊥AB;
为何值时,CD⊥AB;
(2)求二面角S-BC-A的余弦值大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,已知正四棱锥P-ABCD的所有棱长都是2,底面正方形两条对角线相交于O点,M是侧棱PC的中点.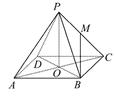
(1)求此正四棱锥的体积.
(2)求直线BM与侧面PAB所成角θ的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com