
分析 根据二次函数的大小求出函数的对称轴,通过讨论t的范围,求出函数的最小值即可.
解答 解:函数f(x)=(x-1)2+1对称轴方程为x=1,
顶点坐标为(1,1),图象开口向上,
若顶点横坐标在区间[t,t+1]左侧时,
有1<t,此时,当x=t时,函数取得最小值$f{(x)_{min}}=f(t)={(t-1)^2}+1$.
若顶点横坐标在区间[t,t+1]上时,
有t≤1≤t+1,即0≤t≤1.当x=1时,函数取得最小值f(x)min=f(1)=1.
若顶点横坐标在区间[t,t+1]右侧时,
有t+1<1,即t<0.当x=t+1时,函数取得最小值$f{(x)_{min}}=f(t+1)={t^2}+1$
综上讨论,$f{(x)_{min}}=\left\{\begin{array}{l}{(t-1)^2}+1,t>1\\ 1,\;\;\;\;\;\;\;\;\;\;\;0≤t≤1\\{t^2}+1\;\;\;\;\;\;t<0\end{array}\right.$.
点评 本题考查了二次函数的性质,考查函数的最值问以及分类讨论思想,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
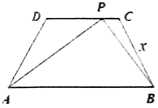 如图,等腰梯形的下底边AB=2,上底边CD=1,两腰AD=BC=1,动点P从点B开始沿着边BC,CD与DA运动,记动点P的轨迹长度为x,将点P到A,B两点距离之和表示为x的函数f(x),则f(x)的图象大致为( )
如图,等腰梯形的下底边AB=2,上底边CD=1,两腰AD=BC=1,动点P从点B开始沿着边BC,CD与DA运动,记动点P的轨迹长度为x,将点P到A,B两点距离之和表示为x的函数f(x),则f(x)的图象大致为( )| A. |  | B. | 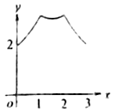 | C. | 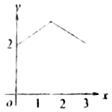 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1004 | B. | 2026 | C. | 4072 | D. | 22016-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $3\sqrt{7}$ | B. | $2\sqrt{6}$ | C. | $5\sqrt{2}$ | D. | $2\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com