
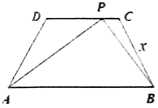
 如图,等腰梯形的下底边AB=2,上底边CD=1,两腰AD=BC=1,动点P从点B开始沿着边BC,CD与DA运动,记动点P的轨迹长度为x,将点P到A,B两点距离之和表示为x的函数f(x),则f(x)的图象大致为( )
如图,等腰梯形的下底边AB=2,上底边CD=1,两腰AD=BC=1,动点P从点B开始沿着边BC,CD与DA运动,记动点P的轨迹长度为x,将点P到A,B两点距离之和表示为x的函数f(x),则f(x)的图象大致为( )| A. |  | B. | 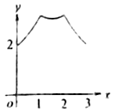 | C. | 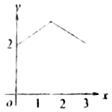 | D. |  |
分析 根据等腰梯形的知识得到∠ABC=∠DAC=60°,等腰梯形的高为$\frac{\sqrt{3}}{2}$,根据余弦定理即可表示AP,继而得到,f(x)=x+$\sqrt{(x-1)^{2}+3}$,0≤x≤1,再根据题意分别求出点P在几个特殊点的位置时,f(x)的值,比较其大小,得到函数的变化趋势,即可判断.
解答 解:∵等腰梯形的下底边AB=2,上底边CD=1,两腰AD=BC=1,
∴∠ABC=∠DAC=60°,等腰梯形的高为$\frac{\sqrt{3}}{2}$
①当P在BC上运动时,由余弦定理可得
AP2=AB2+BP2-2AB•BP•cos60°=4+x2-2•x•2•$\frac{1}{2}$=x2+4-2x=(x-1)2+3
∴f(x)=x+$\sqrt{(x-1)^{2}+3}$
当x=0时,f(0)=2,
当x=1时,f(1)=1+$\sqrt{3}$,
②当点P在CD上运动时,假如运动到CD的中点时,此时AP=$\frac{\sqrt{7}}{2}$,BP=$\frac{\sqrt{7}}{2}$,则f(1.5)=$\sqrt{7}$,
③当点P在运动点D时,此时f(2)=f(1)=1+$\sqrt{3}$,
④当点P在运动点A时,此时f(3)=f(0)=2,
∵1+$\sqrt{3}$>$\sqrt{7}$>2,
∴f(1)=f(2)>f(1.5)>f(0)=f(3),
∴函数f(x)先增大,再减少,再增大,再减少,且变化不是直线型,
故选:B.
点评 本题主要考查函数图象的识别和判断,根据条件先求出0≤x≤1时的解析式是解决本题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,+∞) | B. | [2,4] | C. | [0,4] | D. | (2,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 3 | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | [0,+∞) | C. | (-∞,0) | D. | (-∞,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1]∪(3,+∞) | B. | [1,3) | C. | [1,3] | D. | (-∞,1]∪[3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com