【题目】已知数列{an}满足a1=1，an+1= 
（n∈N*），若bn+1=（n﹣2λ）（ 
+1）（n∈N*），b1=﹣λ，且数列{bn}是单调递增数列，則实数λ的取值范围是（ ）
A.
B.
C.
D.
【答案】C
【解析】解：由an+1= 
得， 
则， 
+1=2（ 
+1）
由a1=1，得 
+1=2，
∴数列{ +1}是首项为2，公比为2的等比数列，
∴ +1=2×2n﹣1=2n ，
由bn+1=（n﹣2λ）（ +1）=（n﹣2λ）2n ，
∵b1=﹣λ，
b2=（1﹣2λ）2=2﹣4λ，
由b2＞b1 ， 得2﹣4λ＞﹣λ，得λ＜ 
，
此时bn+1=（n﹣2λ）2n为增函数，满足题意．
∴实数λ的取值范围是（﹣∞， ）．
故选：C
由数列递推式得到{ +1}是首项为2，公比为2的等比数列，求出其通项公式后代入bn+1=（n﹣2λ）2n ， 由b2＞b1求得实数λ的取值范围，验证满足bn+1=（n﹣2λ）2n为增函数得答案．
科目：高中数学 来源： 题型：
【题目】已知直线 
是椭圆 
的右准线，若椭圆的离心率为 
，右准线方程为x=2．
（1）求椭圆Γ的方程；
（2）已知一直线AB过右焦点F（c，0），交椭圆Γ于A，B两点，P为椭圆Γ的左顶点，PA，PB与右准线交于点M（xM ， yM），N（xN ， yN），问yMyN是否为定值，若是，求出该定值，否则说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）= 
+aln（x﹣1）（a∈R）．
（1）若函数f（x）在区间[2，+∞）上是单调递增函数，试求实数a的取值范围；
（2）当x∈[2，+∞）时，求证： 
≤2ln（x﹣1）≤2x﹣4；
（3）求证： 
+ 
+…+ 
＜lnn＜1+ 
+…+ 
（n∈N*且n≥2）．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在我国古代著名的数学专著《九章算术》里有一段叙述：今有良马与驽马发长安至齐，齐去长安一千一百二十五里，良马初日行一百零三里，日增十三里；驽马初日行九十七里，日减半里；良马先至齐，复还迎驽马，二马相逢．问：几日相逢？（ ）
A.9日
B.8日
C.16日
D.12日
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在△ABC中，角A，B，C的对边分别是a，b，c，且 
acosC=（2b﹣ c）cosA．
（1）求角A的大小；
（2）求cos（ 
﹣B）﹣2sin2 
的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=|cosx|sinx，给出下列五个说法： ①f（ 
π）=﹣ 
；
②若|f（x1）|=|f（x2）|，则x1=x2+kπ（k∈Z）；
③f（x）在区间[﹣ 
， ]上单调递增；
④函数f（x）的周期为π．
⑤f（x）的图象关于点（ 
，0）成中心对称．
其中正确说法的序号是 ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设f（x）是定义在（﹣π，0）∪（0，π）的奇函数，其导函数为f'（x），且 
，当x∈（0，π）时，f'（x）sinx﹣f（x）cosx＜0，则关于x的不等式 
的解集为（ ）
A.
B.
??
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】等腰△ABC中，AC=BC= 
，AB=2，E、F分别为AC、BC的中点，将△EFC沿EF折起，使得C到P，得到四棱锥P﹣ABFE，且AP=BP= 
． 
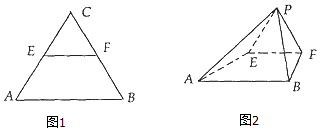
（1）求证：平面EFP⊥平面ABFE；
（2）求二面角B﹣AP﹣E的大小．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}是等比数列，Sn为数列{an}的前n项和，且a3=3，S3=9
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设bn=log2 
，且{bn}为递增数列，若cn= 
，求证：c1+c2+c3+…+cn＜1．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com