
分析 由二项式系数的性质结合已知求得n,写出二项展开式的通项,再由x的指数等于0求得r值,则展开式中的常数项可求.
解答 解:∵${({x^2}-\frac{2}{x})^n}$的二项展开式中,所有项的二项式系数和为64,∴2n=64,即n=6.
则${({x^2}-\frac{2}{x})^n}$=$({x}^{2}-\frac{2}{x})^{6}$,
由${T}_{r+1}={C}_{6}^{r}{(x}^{2})^{6-r}•(-\frac{2}{x})^{r}$=$(-2)^{r}•{C}_{6}^{r}•{x}^{12-3r}$.
令12-3r=0,得r=4.
∴展开式中的常数项为$(-2)^{4}•{C}_{6}^{4}=240$.
故答案为:240.
点评 本题考查二项式定理的应用,考查了二项式系数的性质,关键是对二项展开式通项的记忆与运用,是基础题.


科目:高中数学 来源: 题型:选择题
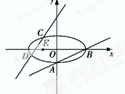 如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{6}}{3}$,过点A(0,-b)和B(a,0)的直线与原点的距离为$\frac{\sqrt{3}}{2}$.已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C,D两点.存在k的值,使以CD为直径的圆过E点,则k=( )
如图,已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{6}}{3}$,过点A(0,-b)和B(a,0)的直线与原点的距离为$\frac{\sqrt{3}}{2}$.已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C,D两点.存在k的值,使以CD为直径的圆过E点,则k=( )| A. | $\frac{7}{6}$ | B. | -$\frac{7}{6}$ | C. | 3 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∧(¬q)是真命题 | D. | 命题p∨(¬q)是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | -$\frac{\sqrt{6}}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{25}{7}$ | B. | $\frac{5}{7}$ | C. | 5 | D. | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,0) | B. | (-1,0) | C. | $(-\frac{6}{5},-\frac{2}{5})$ | D. | (0,-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com