
(本小题满分14分)
(1)已知正项等差数列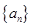 的前
的前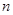 项和为
项和为 ,若
,若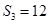 ,且
,且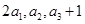 成等比数列.求
成等比数列.求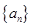 的通项公式.
的通项公式.
(2)数列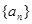 中,
中,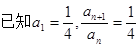 ,
, .求
.求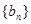 的通项公式.
的通项公式.
(1)  ; (2)
; (2) 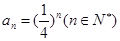 ,
, .
.
解析试题分析:(1)根据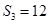 ,且
,且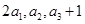 成等比数列可得到关于a1和d的两个方程,进而得到
成等比数列可得到关于a1和d的两个方程,进而得到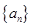 的通项公式.
的通项公式.
(2) 由 ,可知数列
,可知数列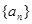 是首项为
是首项为 ,公比为
,公比为 的等比数列,因而可求出
的等比数列,因而可求出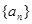 的通项公式,进一步根据对数的运算性质可求出bn.
的通项公式,进一步根据对数的运算性质可求出bn.
(1)记 的公差为
的公差为
∵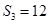 ,即
,即 ∴
∴ ,所以
,所以 ·······2分
·······2分
又 ,
, ,
,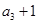 成等比数列,
成等比数列,
∴ ,即
,即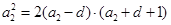 ·······4分
·······4分
解得, 或
或 (舍去),
(舍去),
∴ ,故
,故 ·······7分
·······7分
(2) 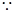

∴数列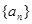 是首项为
是首项为 ,公比为
,公比为 的等比数列 ·······2分
的等比数列 ·······2分
故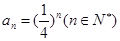 ·······4分
·······4分 ·······5分
·······5分
∴ . ·······7分
. ·······7分
考点:等差数列的前n项和,等比数列的定义,对数的运算性质.
点评:利用方程的思想来考虑如何求a1和d.这样须建立关于它们俩个的两个方程.由于 显然可确定
显然可确定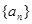 是首项为
是首项为 ,公比为
,公比为 的等比数列,到此问题基本得解.
的等比数列,到此问题基本得解.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知数列 的各项排成如图所示的三角形数阵,数阵中每一行的第一个数
的各项排成如图所示的三角形数阵,数阵中每一行的第一个数 构成等差数列
构成等差数列 ,
, 是
是 的前n项和,且
的前n项和,且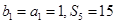

( I )若数阵中从第三行开始每行中的数按从左到右的顺序均构成公比为正数的等比数列,且公比相等,已知 ,求
,求 的值;
的值;
(Ⅱ)设 ,求
,求 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com