
(本小题满分12分)
已知数列 的各项排成如图所示的三角形数阵,数阵中每一行的第一个数
的各项排成如图所示的三角形数阵,数阵中每一行的第一个数 构成等差数列
构成等差数列 ,
, 是
是 的前n项和,且
的前n项和,且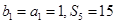

( I )若数阵中从第三行开始每行中的数按从左到右的顺序均构成公比为正数的等比数列,且公比相等,已知 ,求
,求 的值;
的值;
(Ⅱ)设 ,求
,求 .
.
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
已知数列 的前
的前 项和为
项和为 ,且满足
,且满足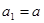 (
(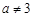 ),
),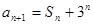 ,设
,设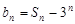 ,
,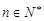 .
.
(1)求证:数列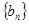 是等比数列;
是等比数列;
(2)若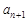 ≥
≥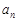 ,
,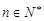 ,求实数
,求实数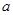 的最小值;
的最小值;
(3)当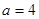 时,给出一个新数列
时,给出一个新数列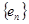 ,其中
,其中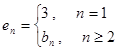 ,设这个新数列的前
,设这个新数列的前 项和为
项和为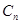 ,若
,若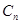 可以写成
可以写成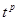 (
(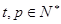 且
且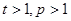 )的形式,则称
)的形式,则称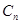 为“指数型和”.问
为“指数型和”.问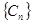 中的项是否存在“指数型和”,若存在,求出所有“指数型和”;若不存在,请说明理由.
中的项是否存在“指数型和”,若存在,求出所有“指数型和”;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知等差数列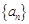 中,
中,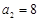 ,前10项的和
,前10项的和
(1)求数列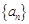 的通项公式;
的通项公式;
(2)若从数列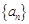 中,依次取出第2、4、8,…,
中,依次取出第2、4、8,…,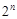 ,…项,按原来的顺序排成一个新的数列
,…项,按原来的顺序排成一个新的数列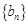 ,试求新数列
,试求新数列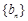 的前
的前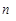 项和
项和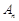 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知三个正整数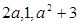 按某种顺序排列成等差数列。
按某种顺序排列成等差数列。
(1)求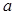 的值;
的值;
(2)若等差数列 的首项、公差都为
的首项、公差都为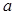 ,等比数列
,等比数列 的首项、公比也都为
的首项、公比也都为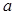 ,前
,前 项和分别为
项和分别为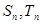 ,且
,且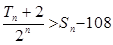 ,求满足条件的正整数
,求满足条件的正整数 的最大值。
的最大值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com