
正四棱锥S-ABCD的侧棱长为 ,底面边长为
,底面边长为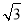 ,E为SA的中点,则异面直线BE和SC所成的角为( ).
,E为SA的中点,则异面直线BE和SC所成的角为( ).

A.30° B.45° C.60° D.90°
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练3-x4练习卷(解析版) 题型:填空题
给出下列四个命题:
①命题“?x∈R,cos x>0”的否定是:“?x∈R,cos x≤0”;
②若lga+lgb=lg(a+b),则a+b的最大值为4;
③定义在R上的奇函数f(x)满足f(x+2)=-f(x),则f(6)的值为0;
④已知随机变量X服从正态分布N(1,σ2),P(X≤5)=0.81,则P(X≤-3)=0.19;其中真命题的序号是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练3-x1练习卷(解析版) 题型:填空题
如图,在△ABC中,AB=AC=2,BC=2  ,点D在BC边上,∠ADC=75°,则AD的长为________.
,点D在BC边上,∠ADC=75°,则AD的长为________.

查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练3-x1练习卷(解析版) 题型:选择题
已知双曲线C1: =1(a>0,b>0)的离心率为2,若抛物线C2:x2=2py(p>0)的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为( ).
=1(a>0,b>0)的离心率为2,若抛物线C2:x2=2py(p>0)的焦点到双曲线C1的渐近线的距离为2,则抛物线C2的方程为( ).
A.x2= y B.x2=
y B.x2= y
y
C.x2=8y D.x2=16y
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练3-d4练习卷(解析版) 题型:解答题
如图,在四棱锥P-ABCD中,已知PB⊥底面ABCD,BC⊥AB,AD∥BC,AB=AD=2,CD⊥PD,异面直线PA和CD所成角等于60°.

(1)求证:面PCD⊥面PBD;
(2)求直线PC和平面PAD所成角的正弦值的大小;
(3)在棱PA上是否存在一点E,使得二面角A-BE-D的余弦值为 ?若存在,指出点E在棱PA上的位置,若不存在,说明理由.
?若存在,指出点E在棱PA上的位置,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练3-d3练习卷(解析版) 题型:解答题
已知数列{an}满足a1=3,an+1=an+p·3n(n∈N*,p为常数),a1,a2+6,a3成等差数列.
(1)求p的值及数列{an}的通项公式;
(2)设数列{bn}满足bn=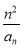 ,证明:bn≤
,证明:bn≤ .
.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练1-9练习卷(解析版) 题型:填空题
已知双曲线 =1(a>0,b>0)的一条渐近线与直线x+2y-1=0垂直,则双曲线的离心率等于________.
=1(a>0,b>0)的一条渐近线与直线x+2y-1=0垂直,则双曲线的离心率等于________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练1-7练习卷(解析版) 题型:填空题
已知O是坐标原点,点M的坐标为(2,1),若点N(x,y)为平面区域 上的一个动点,则
上的一个动点,则 的最大值是________.
的最大值是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com