
已知数列{an}满足a1=3,an+1=an+p·3n(n∈N*,p为常数),a1,a2+6,a3成等差数列.
(1)求p的值及数列{an}的通项公式;
(2)设数列{bn}满足bn=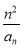 ,证明:bn≤
,证明:bn≤ .
.
(1)an=3n(2)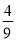
【解析】由a1=3,an+1=an+p·3n,得a2=3+3p,a3=a2+9p=3+12p.
∵a1,a2+6,a3成等差数列,∴a1+a3=2(a2+6),即3+3+12p=2(3+3p+6),得p=2.
依题意知,an+1=an+2×3n,
当n≥2时,a2-a1=2×31,a3-a2=2×32,…,an-an-1=2×3n-1.
等号两边分别相加得an-a1=2(31+32+…+3n-1)=2×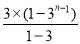 =3n-3,
=3n-3,
∴an-a1=3n-3,∴an=3n(n≥2).
又a1=3适合上式,故an=3n.
(2)证明:∵an=3n,∴bn=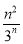 .
.
∵bn+1-bn=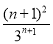 -
-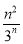 =
=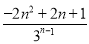 (n∈N*).
(n∈N*).
若-2n2+2n+1<0,则n> ,
,
即当n≥2时,有bn+1<bn.
又因为b1=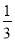 ,b2<
,b2<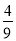 .故bn≤
.故bn≤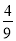


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练倒数第10天练习卷(解析版) 题型:选择题
已知集合M={a,b,c},集合N满足N⊆M,则集合N的个数是( ).
A.6 B.7 C.8 D.9
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练3-x4练习卷(解析版) 题型:选择题
已知某8个数的平均数为5,方差为2,现又加入一个新数据5,此时这9个数的平均数为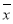 ,方差为s2,则( ).
,方差为s2,则( ).
A.  =5,s2<2 B.
=5,s2<2 B.  =5,s2>2 C.
=5,s2>2 C.  >5,s2<2 D.
>5,s2<2 D.  >5,s2>2
>5,s2>2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练3-x1练习卷(解析版) 题型:选择题
正四棱锥S-ABCD的侧棱长为 ,底面边长为
,底面边长为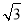 ,E为SA的中点,则异面直线BE和SC所成的角为( ).
,E为SA的中点,则异面直线BE和SC所成的角为( ).

A.30° B.45° C.60° D.90°
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练3-d4练习卷(解析版) 题型:解答题
设数列{an}的前n项和为Sn,a1=1,且对任意正整数n,点(an+1,Sn)在直线3x+2y-3=0上.
(1)求数列{an}的通项公式;
(2)是否存在实数λ,使得数列 为等差数列?若存在,求出λ的值;若不存在,则说明理由.
为等差数列?若存在,求出λ的值;若不存在,则说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练2-2练习卷(解析版) 题型:解答题
某次考试中,从甲,乙两个班各抽取10名学生的成绩进行统计分析,两班10名学生成绩的茎叶图如图所示,成绩不小于90分为及格.

(1)从每班抽取的学生中各抽取一人,求至少有一个及格的概率;
(2)从甲班10人中取两人,乙班10人中取一人,三人中及格人数记为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练2-1练习卷(解析版) 题型:解答题
在△ABC中,角A,B,C的对边分别为a,b,c,已知角A= , sin B=3sin C.
, sin B=3sin C.
(1)求tan C的值;
(2)若a= ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练1-9练习卷(解析版) 题型:填空题
如图,椭圆 =1(a>b>0)的左、右焦点为F1,F2,上顶点为A,离心率为
=1(a>b>0)的左、右焦点为F1,F2,上顶点为A,离心率为 ,点P为第一象限内椭圆上的一点,若S△PF1A∶S△PF1F2=2∶1,则直线PF1的斜率为________.
,点P为第一象限内椭圆上的一点,若S△PF1A∶S△PF1F2=2∶1,则直线PF1的斜率为________.

查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练1-7练习卷(解析版) 题型:选择题
已知集合A= ,B={x||x-1|≤1},则A∩B=( ).
,B={x||x-1|≤1},则A∩B=( ).
A.{-1,0} B.{0,1} C.{0} D.{1}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com