练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，在△ABC中，AB＝AC＝2，BC＝2 ，点D在BC边上，∠ADC＝75°，则AD的长为________．

     

     

    －

    【解析】在△ABC中，因为AB＝AC＝2，BC＝2 ，所以∠C＝30°，又∠ADC＝75°，所以∠DAC＝75°，所以CD＝CA＝2，由余弦定理得：AD2＝CD2＋AC2－2CD×AC×cos C＝8－4 .所以AD＝－.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学（理）二轮复习体系通关训练倒数第3天练习卷（解析版） 题型：选择题

    已知双曲线kx2－y2＝1的一条渐近线与直线l：2x＋y＋1＝0垂直，则此双曲线的离心率是(　　)．

    A. B. C．4 D.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习体系通关训练3-x5练习卷（解析版） 题型：填空题

    以双曲线＝1的右焦点为圆心，且被其中一条渐近线截得的弦长为6的圆的标准方程为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习体系通关训练3-x4练习卷（解析版） 题型：选择题

    在区间[1,5]和[2,4]分别取一个数，记为a，b，则方程＝1表示焦点在x轴上且离心率小于的椭圆的概率为(　　)．

    A. B. C. D.

    答案　

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习体系通关训练3-x4练习卷（解析版） 题型：选择题

    已知某8个数的平均数为5，方差为2，现又加入一个新数据5，此时这9个数的平均数为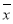，方差为s2，则(　　)．

    A. ＝5，s2<2 B. ＝5，s2>2 C. >5，s2<2 D. >5，s2>2

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习体系通关训练3-x1练习卷（解析版） 题型：选择题

    已知两条不重合的直线m，n和两个不重合的平面α，β，有下列命题：

    ①若m⊥n，m⊥α，则n∥α；②若m⊥α，n⊥β，m∥n，则α∥β；③若m，n是两条异面直线，m?α，n?β，m∥β，n∥α，则α∥β；④若α⊥β，α∩β＝m，n?β，n⊥m，则n⊥α；其中正确命题的个数是(　　)．

    A．1 B．2 C．3 D．4

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习体系通关训练3-x1练习卷（解析版） 题型：选择题

    正四棱锥S-ABCD的侧棱长为，底面边长为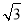，E为SA的中点，则异面直线BE和SC所成的角为(　　)．

    A．30° B．45° C．60° D．90°

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习体系通关训练2-2练习卷（解析版） 题型：解答题

    某次考试中，从甲，乙两个班各抽取10名学生的成绩进行统计分析，两班10名学生成绩的茎叶图如图所示，成绩不小于90分为及格．

    (1)从每班抽取的学生中各抽取一人，求至少有一个及格的概率；

    (2)从甲班10人中取两人，乙班10人中取一人，三人中及格人数记为X，求X的分布列和数学期望．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学（理）二轮复习体系通关训练1-8练习卷（解析版） 题型：填空题

    一空间几何体的三视图如图所示，该几何体的体积为16π＋，则图中x的值为________．

     

     

    查看答案和解析>>

    同步练习册答案