
如图,在四棱锥P-ABCD中,已知PB⊥底面ABCD,BC⊥AB,AD∥BC,AB=AD=2,CD⊥PD,异面直线PA和CD所成角等于60°.

(1)求证:面PCD⊥面PBD;
(2)求直线PC和平面PAD所成角的正弦值的大小;
(3)在棱PA上是否存在一点E,使得二面角A-BE-D的余弦值为 ?若存在,指出点E在棱PA上的位置,若不存在,说明理由.
?若存在,指出点E在棱PA上的位置,若不存在,说明理由.
(1)见解析(2)存在
【解析】(1)证明:PB⊥底面ABCD,∴PD⊥CD,
又∵CD⊥PD,PD∩PB=P,PD,PB?平面PBD.
∴CD⊥平面PBD,又CD?平面PCD,
∴平面PCD⊥平面PBD.
(2)如图,以B为原点,BA,BC,BP所在直线分别为x,y,z轴,建立空间直角坐标系,
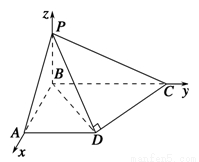
设BC=a,BP=b,则B(0,0,0),A(2,0,0),C(0,a,0),
D(2,2,0),P(0,0,b).
∵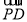 =(2,2,-b),
=(2,2,-b),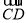 =(2,2-a,0),CD⊥PD,
=(2,2-a,0),CD⊥PD,
∴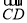 ·
·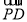 =0,∴4+4-2a=0,a=4,
=0,∴4+4-2a=0,a=4,
又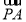 =(2,0,-b),
=(2,0,-b),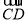 =(2,-2,0),
=(2,-2,0),
异面直线PA和CD所成角等于60°,
∴ =
=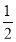 ,
,
即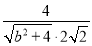 =
=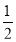 ,解得b=2,
,解得b=2,
 =(0,4,-2),
=(0,4,-2), =(0,2,0),
=(0,2,0),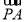 =(2,0,-2).
=(2,0,-2).
设平面PAD的一个法向量为n1=(x1,y1,z1),
则由 得
得
取n1=(1,0,1),
∵sin θ=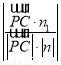 =
=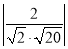 =
=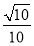 ,∴直线PC和平面PAD所成角的正弦值为
,∴直线PC和平面PAD所成角的正弦值为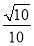 .
.
(3)解 假设存在,设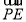 =λ
=λ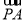 ,且E(x,y,z),则(x,y,z-2)=λ(2,0,-2),E(2λ,0,2-2λ),设平面DEB的一个法向量为n2=(x2,y2,z2),
,且E(x,y,z),则(x,y,z-2)=λ(2,0,-2),E(2λ,0,2-2λ),设平面DEB的一个法向量为n2=(x2,y2,z2),
则由 得
得
取n2=(λ-1,1-λ,λ),
又平面ABE的法向量n3=(0,1,0),
由cos θ=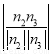 =
=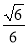 ,得
,得 =
=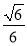 ,解得λ=
,解得λ=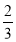 或λ=2(不合题意).
或λ=2(不合题意).
∴存在这样的E点,E为棱PA上的靠近A的三等分点.


科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练倒数第10天练习卷(解析版) 题型:选择题
如图是一个算法的程序框图,当输入的x值为-9时,其输出的结果( ).

A.-9 B.1 C.3 D.6
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练3-x4练习卷(解析版) 题型:选择题
在区间[1,5]和[2,4]分别取一个数,记为a,b,则方程 =1表示焦点在x轴上且离心率小于
=1表示焦点在x轴上且离心率小于 的椭圆的概率为( ).
的椭圆的概率为( ).
A. B.
B.  C.
C.  D.
D. 
答案
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练3-x1练习卷(解析版) 题型:选择题
已知两条不重合的直线m,n和两个不重合的平面α,β,有下列命题:
①若m⊥n,m⊥α,则n∥α;②若m⊥α,n⊥β,m∥n,则α∥β;③若m,n是两条异面直线,m?α,n?β,m∥β,n∥α,则α∥β;④若α⊥β,α∩β=m,n?β,n⊥m,则n⊥α;其中正确命题的个数是( ).
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练3-x1练习卷(解析版) 题型:选择题
正四棱锥S-ABCD的侧棱长为 ,底面边长为
,底面边长为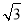 ,E为SA的中点,则异面直线BE和SC所成的角为( ).
,E为SA的中点,则异面直线BE和SC所成的角为( ).

A.30° B.45° C.60° D.90°
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练3-d3练习卷(解析版) 题型:解答题
已知抛物线C:y2=2px(p>0),M点的坐标为(12,8),N点在抛物线C上,且满足 =
= ,O为坐标原点.
,O为坐标原点.

(1)求抛物线C的方程;
(2)以M点为起点的任意两条射线l1,l2的斜率乘积为1,并且l1与抛物线C交于A,B两点,l2与抛物线C交于D,E两点,线段AB,DE的中点分别为G,H两点.求证:直线GH过定点,并求出定点坐标.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练2-2练习卷(解析版) 题型:解答题
某次考试中,从甲,乙两个班各抽取10名学生的成绩进行统计分析,两班10名学生成绩的茎叶图如图所示,成绩不小于90分为及格.

(1)从每班抽取的学生中各抽取一人,求至少有一个及格的概率;
(2)从甲班10人中取两人,乙班10人中取一人,三人中及格人数记为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练1-9练习卷(解析版) 题型:选择题
已知抛物线y2=2px(p>0)的焦点F与双曲线 =1的右焦点重合,抛物线的准线与x轴的交点为K,点A在抛物线上且|AK|=
=1的右焦点重合,抛物线的准线与x轴的交点为K,点A在抛物线上且|AK|= |AF|,则A点的横坐标为( ).
|AF|,则A点的横坐标为( ).
A.2 B.3 C.2
B.3 C.2 D.4
D.4
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(理)二轮复习体系通关训练1-7练习卷(解析版) 题型:选择题
设z=x+y,其中实数x,y满足 若z的最大值为6,则z的最小值为( ).
若z的最大值为6,则z的最小值为( ).
A.-3 B.-2 C.-1 D.0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com