
设有关于x的一元二次方程x2+2ax+b2=0. (l)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求方程有实根的概率;(2)若a是从区间[0,t+1]任取的一个数,b是从区间[0,t]任取的一个数,其中t满足2≤t≤3,求方程有实根的概率,并求出其概率的最大值.
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)本小题为古典概型求概率的问题,先求出a与b构成的实数对(a,b)总个数即基本事件的总数,再一一进行检验符合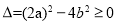 的实数对即可求出其概率;(2)本小题为几何概型求概率的问题,由0≤a≤t+1,0≤b≤t利用线性规划的知识(a看直角坐标系中的x,b看成直角坐标系中的y)可画出如下图的矩形,又a≥b(即为y≤x区域)则符合条件的阴影部分区域为梯形,因此所求的概率为
的实数对即可求出其概率;(2)本小题为几何概型求概率的问题,由0≤a≤t+1,0≤b≤t利用线性规划的知识(a看直角坐标系中的x,b看成直角坐标系中的y)可画出如下图的矩形,又a≥b(即为y≤x区域)则符合条件的阴影部分区域为梯形,因此所求的概率为 ,其次根据t的范围利用不等式的性质求出P的范围即可找到其最大值.
,其次根据t的范围利用不等式的性质求出P的范围即可找到其最大值.
试题解析:(1)总的基本事件有12个,即a,b构成的实数对(a,b)有(0,0),(0,1),(0,2),(1,0),(1,1),(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2).设事件A为“方程有实根”,包含的基本事件有(0,0),(1,0),(1,1),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2)共9个,所以事件A的概率为P(A)= =
= ;
;
(2)a,b构成的实数对(a,b)满足条件有0≤a≤t+1,0≤b≤t,a≥b,设事件B为“方程有实根”,则此事件满足几何概型. 如图,
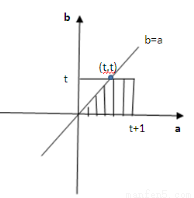
 ,∵2≤t≤3,∴3≤t+1≤4,即
,∵2≤t≤3,∴3≤t+1≤4,即 ,所以
,所以 ,即
,即 ≤P(B)≤
≤P(B)≤ ,所以其概率的最大值为
,所以其概率的最大值为 .
.
考点:古典概型的概率公式,几何概型的概率公式,一元二次方程根的判别式,线性规划问题,不等式的性质,化归思想.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源:2016届河南省实验学校高一下学期期末数学试卷1(解析版) 题型:选择题
某班5次数学测验中,甲、乙两同学的成绩如下: ( )
甲:90 82 88 96 94; 乙:94 86 88 90 92
A.甲的平均成绩比乙好
B.甲的平均成绩比乙差
C.甲乙平均分相同,甲的成绩稳定性比乙好
D.甲乙平均分相同,乙的成绩稳定性比甲好
查看答案和解析>>
科目:高中数学 来源:2016届河南省周口市高一下学期期末考试数学试卷(解析版) 题型:填空题
给出下列说法:①终边在y轴上的角的集合是 ,
,
②若函数f(x)=asin2x+btanx+2,且f(-3)=5,则f(3)的值为-1,
③函数y=ln|x-1|的图象与函数y=-2cos?x(-2≤x≤4}的图像所有交点的横坐标之和等于6;
其中正确的说法是__________〔写出所有正确说法的序号).
查看答案和解析>>
科目:高中数学 来源:2016届河南省周口市高一下学期期末考试数学试卷(解析版) 题型:选择题
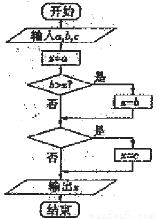
如图的程序框图,如果输入三个实数a,b,c,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入下面四个选项中的( ).
A.c>x? B.x>c? C.c>b? D.b>c?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com