
分析 (Ⅰ)假设方程f(x)-x=0存在两个实数根α,β(α≠β),不妨设α<β,得到f'(c)=1,与已知0<f'(x)<1矛盾,假设不成立;
(Ⅱ)求出函数f(x)-x为减函数,得到|f(x3)-f(x2)|<|x3-x2|,判断出-1<x1-x2<1,|x3-x1|<1和-1<x3-x1<1,相加即可.
解答 (Ⅰ)证明:假设方程f(x)-x=0存在两个实数根α,β(α≠β),
则f(α)-α=0,f(β)-β=0.…(2分)
不妨设α<β,根据题意存在c∈(α,β),
满足f(β)-f(α)=(β-α)f'(c).
因为f(α)=α,f(β)=β,且α≠β,所以f'(c)=1.…(5分)
与已知0<f'(x)<1矛盾.又f(x)-x=0有实数根,
所以方程f(x)-x=0有且只有一个实数根.…(6分)
(Ⅱ)解:当x2=x3时,结论显然成立;…(7分)
当x2≠x3,不妨设a<x2<x3<b.
因为x∈(a,b),且f'(x)>0,所以f(x)为增函数,那么f(x2)<f(x3).
又因为f'(x)-1<0,所以函数f(x)-x为减函数,…(9分)
所以f(x2)-x2>f(x3)-x3.
所以0<f(x3)-f(x2)<x3-x2,即|f(x3)-f(x2)|<|x3-x2|.…(10分)
因为|x2-x1|<1,所以-1<x1-x2<1,(1)
又因为|x3-x1|<1,所以-1<x3-x1<1,(2)
(1)+(2)得-2<x2-x3<2即|x3-x2|<2.…(12分)
所以|f(x3)-f(x2)|<|x3-x2|<2.…(13分)
综上,对于任意符合条件的x1,x2,x3总有|f(x3)-f(x2)|<2成立.…(14分)
点评 本题考查了新定义问题,考查反证法的应用以及函数的单调性问题,考查绝对值的应用,是一道中档题.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
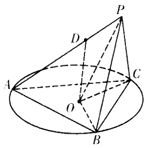 如图所示,正三角形ABC的外接圆半径为2,圆心为O,PB=PC=2,D为AP上一点,AD=2DP,点D在平面ABC内的射影为圆心O.
如图所示,正三角形ABC的外接圆半径为2,圆心为O,PB=PC=2,D为AP上一点,AD=2DP,点D在平面ABC内的射影为圆心O.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com