
分析 (1)设切点,利用函数h(x)=aex的一条切线为y=ex,求a的值
(2)即证明1>(1+x+$\frac{1}{2}$x2)e-x(x>0),构造函数,即可证明.
解答 (1)解:根据题意可设切点为(x0,y0)
则$a{e}^{{x}_{0}}$=ex0,$a{e}^{{x}_{0}}$=e,
故a=1;
(2)证明:当x>0时,h(x)>1+x+$\frac{1}{2}$x2,即ex>1+x+$\frac{1}{2}$x2,
则1>(1+x+$\frac{1}{2}$x2)e-x(x>0)
令g(x)=(1+x+$\frac{1}{2}$x2)e-x,并求其最大值.
则g′(x)=(-$\frac{1}{2}$x2)e-x.
所以在x>0,g(x)恒减,所以g(x)<g(0)=1,
故h(x)>1+x+$\frac{1}{2}$x2.
点评 本题考查导数知识的运用,考查导数的几何运用,考查不等式的证明,正确转化是关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 队员编号 | 1 | 2 | 3 | 4 | 5 |
| 甲班成绩 | 31 | 34 | 33 | 29 | 28 |
| 乙班成绩 | 27 | 31 | 30 | X | 31 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,2,3} | B. | {0,3,5} | C. | {0,1,2,3} | D. | {0,2,3,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
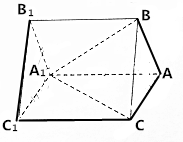 在三棱柱ABC-A1B1C1中已知AB=AC=AA1=2,∠BAA1=∠CAA1=60°,异面直线A1C1与BC成角为45°.
在三棱柱ABC-A1B1C1中已知AB=AC=AA1=2,∠BAA1=∠CAA1=60°,异面直线A1C1与BC成角为45°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com