
ЎҫМвДҝЎҝТСЦӘДіГсЧеЖ·ЕЖКЦ»ъЙъІъЙМОӘУӯәПКРіЎРиЗуЈ¬ГҝДк¶ј»бСР·ўНЖіцТ»ҝоРВРНәЕКЦ»ъ.ёГ№«ЛҫПЦСР·ўБЛТ»ҝоРВРНЦЗДЬКЦ»ъІўН¶ИлЙъІъЈ¬ЙъІъХвҝоКЦ»ъөДФВ№М¶ЁіЙұҫОӘ80НтФӘЈ¬ГҝЙъІъ1З§МЁЈ¬РлБнН¶Ил27НтФӘЈ¬ ЙиёГ№«ЛҫГҝФВЙъІъ![]() З§МЁІўДЬИ«ІҝПъКЫНкЈ¬Гҝ1З§МЁөДПъКЫКХИлОӘ
З§МЁІўДЬИ«ІҝПъКЫНкЈ¬Гҝ1З§МЁөДПъКЫКХИлОӘ![]() НтФӘЈ¬ЗТ
НтФӘЈ¬ЗТ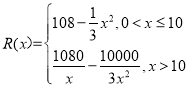 .ОӘёьәГНЖ№гёГІъЖ·Ј¬КЦ»ъЙъІъЙМГҝФВ»№Ц§ё¶ёчАа№гёж·СУГ20НтФӘ.
.ОӘёьәГНЖ№гёГІъЖ·Ј¬КЦ»ъЙъІъЙМГҝФВ»№Ц§ё¶ёчАа№гёж·СУГ20НтФӘ.
ЈЁўсЈ©РҙіцФВАыИу![]() ЈЁНтФӘЈ©№ШУЪФВІъБҝ
ЈЁНтФӘЈ©№ШУЪФВІъБҝ![]() ЈЁЗ§МЁЈ©өДәҜКэҪвОцКҪЈ»
ЈЁЗ§МЁЈ©өДәҜКэҪвОцКҪЈ»
ЈЁўтЈ©өұФВІъБҝОӘ¶аЙЩЗ§МЁКұЈ¬ёГ№«ЛҫФЪХвТ»РНәЕөДКЦ»ъЙъІъЦРЛщ»сФВАыИуЧоҙу?
Ўҫҙр°ёЎҝЈЁўсЈ©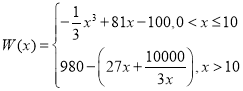 ЈЁўтЈ©9З§МЁ
ЈЁўтЈ©9З§МЁ
ЎҫҪвОцЎҝ
ЈЁўсЈ©КЧПИјЖЛгіцЧЬіЙұҫЈ¬өұ![]() КұЈ¬
КұЈ¬![]() Ј» өұ
Ј» өұ![]() КұЈ¬
КұЈ¬![]() Ј®јҙҝЙөГіцәҜКэөДҪвОцКҪЈ®
Ј®јҙҝЙөГіцәҜКэөДҪвОцКҪЈ®
ЈЁўтЈ©АыУГөјКэСРҫҝәҜКэөДөҘөчРФЈ¬И»әуЗуҪвәҜКэөДЧоЦөјҙҝЙөГЈ®
ҪвЈәЈЁўсЈ©ЙиФВІъБҝ![]() ЈЁЗ§МЁЈ©Ј¬ФтЧЬіЙұҫОӘ
ЈЁЗ§МЁЈ©Ј¬ФтЧЬіЙұҫОӘ![]() НтФӘЈ¬Фт
НтФӘЈ¬Фт![]() Ј¬
Ј¬
Гҝ1З§МЁөДПъКЫКХИлОӘ![]() НтФӘЗТ
НтФӘЗТ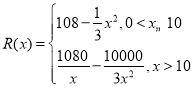 Ј®
Ј®
Фтөұ![]() КұЈ¬
КұЈ¬![]() Ј¬
Ј¬
Фтөұ![]() КұЈ¬
КұЈ¬![]() Ј¬
Ј¬
ЧЫЙПҝЙөГ Ј¬
Ј¬
ЈЁўтЈ©ўЩөұ![]() КұЈ¬УЙ
КұЈ¬УЙ![]() Ј¬
Ј¬
өГөұ![]() КұЈ¬
КұЈ¬![]() Ј¬өҘөчөЭФцЈ»
Ј¬өҘөчөЭФцЈ»
өұ![]() КұЈ¬
КұЈ¬![]() Ј¬өҘөчөЭјхЈ®
Ј¬өҘөчөЭјхЈ®
№К![]() Ј»
Ј»
ўЪөұ![]() КұЈ¬
КұЈ¬![]() Ј¬
Ј¬
өұЗТҪцөұ![]() јҙ
јҙ![]() КұИЎЧоҙуЦө
КұИЎЧоҙуЦө![]()
ЧЫЙПЈ¬өұФВІъБҝОӘ9З§МЁКұЈ¬ёГ№«ЛҫФЪХвТ»РНәЕөДКЦ»ъЙъІъЦРЛщ»сФВАыИуЧоҙуЈ¬АыИу¶оОӘ![]() НтФӘЈ®
НтФӘЈ®


 ЖЪД©іеҙМ100·ЦҙҙРВҪрҫнНкИ«КФҫнПөБРҙр°ё
ЖЪД©іеҙМ100·ЦҙҙРВҪрҫнНкИ«КФҫнПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіРЈі«өјОӘМША§С§ЙъДјҫиЈ¬ТӘЗуФЪЧФ¶Ҝ№әЛ®»ъҙҰГҝ№әВтТ»ЖҝҝуИӘЛ®Ј¬ұгЧФҫхПтҫиҝоПдЦРЦБЙЩН¶ИлТ»ФӘЗ®Ј®ПЦНіјЖБЛБ¬Рш5МмөДКЫіцҝуИӘЛ®ПдКэәНКХИлЗйҝцЈ¬БРұнИзПВЈә
КЫіцЛ®Бҝ | 7 | 6 | 6 | 5 | 6 |
КХИл | 165 | 142 | 148 | 125 | 150 |
ѧУјЖ»®Ҫ«ҫиҝоТФҪұС§ҪрөДРОКҪҪұАшёшЖ·С§јжУЕөДМША§ЙъЈ¬№ж¶ЁЈәМША§ЙъЧЫәПҝјәЛЗ°20ГыЈ¬»сТ»өИҪұС§Ҫр500ФӘЈ»ЧЫәПҝјәЛ21-50ГыЈ¬»с¶юөИҪұС§Ҫр300ФӘЈ»ЧЫәПҝјәЛ50ГыТФәуөДІ»»сөГҪұС§ҪрЈ®
ЈЁ1Ј©Иф![]() Ул
Ул![]() іЙПЯРФПа№ШЈ¬ФтДіМмКЫіц9ПдЛ®КұЈ¬ФӨјЖКХИлОӘ¶аЙЩФӘЈҝ
іЙПЯРФПа№ШЈ¬ФтДіМмКЫіц9ПдЛ®КұЈ¬ФӨјЖКХИлОӘ¶аЙЩФӘЈҝ
ЈЁ2Ј©јЩЙијЧЎўТТЎўұыИэГыС§Йъҫщ»сҪұЈ¬ЗТёчЧФ»сТ»өИҪұәН¶юөИҪұөДҝЙДЬРФПаН¬Ј¬ЗуИэИЛ»сөГҪұС§ҪрЦ®әНІ»і¬№э1000ФӘөДёЕВКЈ®
ёҪЈә»Ш№й·ҪіМ![]() Ј¬ЖдЦР
Ј¬ЖдЦР Ј®
Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіөҘО»ОӘҙЩҪшЦ°№ӨТөОсјјДЬМбЙэЈ¬¶ФёГөҘО»120ГыЦ°№ӨҪшРРТ»ҙОТөОсјјДЬІвКФЈ¬ІвКФПоДҝ№І5По.ПЦҙУЦРЛж»ъійИЎБЛ10ГыЦ°№ӨөДІвКФҪб№ыЈ¬Ҫ«ЛьГЗұаәЕәуөГөҪЛьГЗөДНіјЖҪб№ыИзПВұнЈЁұн1Ј©ЛщКҫЈЁЎ°ЎМЎұұнКҫІвКФәПёсЈ¬Ў°ЎБЎұұнКҫІвКФІ»әПёсЈ©.
ұн1Јә
ұаәЕ\ІвКФПоДҝ | 1 | 2 | 3 | 4 | 5 |
1 | ЎБ | ЎМ | ЎМ | ЎМ | ЎМ |
2 | ЎМ | ЎМ | ЎМ | ЎМ | ЎБ |
3 | ЎМ | ЎМ | ЎМ | ЎМ | ЎБ |
4 | ЎМ | ЎМ | ЎМ | ЎБ | ЎБ |
5 | ЎМ | ЎМ | ЎМ | ЎМ | ЎМ |
6 | ЎМ | ЎБ | ЎБ | ЎМ | ЎБ |
7 | ЎБ | ЎМ | ЎМ | ЎМ | ЎБ |
8 | ЎМ | ЎБ | ЎБ | ЎБ | ЎБ |
9 | ЎМ | ЎМ | ЎБ | ЎБ | ЎБ |
10 | ЎМ | ЎМ | ЎМ | ЎМ | ЎБ |
№ж¶ЁЈәГҝПоІвКФәПёсөГ5·ЦЈ¬І»әПёсөГ0·Ц.
ЈЁ1Ј©ТФійИЎөДХв10ГыЦ°№ӨәПёсПоөДПоКэөДЖөВКҙъМжГҝГыЦ°№ӨәПёсПоөДПоКэөДёЕВК.
ўЩЙиійИЎөДХв10ГыЦ°№ӨЦРЈ¬ГҝГыЦ°№ӨІвКФәПёсөДПоКэОӘ![]() Ј¬ёщҫЭЙПГжөДІвКФҪб№ыНіјЖұнЈ¬БРіц
Ј¬ёщҫЭЙПГжөДІвКФҪб№ыНіјЖұнЈ¬БРіц![]() өД·ЦІјБРЈ¬Іў№АјЖХв120ГыЦ°№ӨөДЖҪҫщөГ·ЦЈ»
өД·ЦІјБРЈ¬Іў№АјЖХв120ГыЦ°№ӨөДЖҪҫщөГ·ЦЈ»
ўЪјЩЙиёчГыЦ°№ӨөДёчПоІвКФҪб№ыПа»Ҙ¶АБўЈ¬ДіҝЖКТУР5ГыЦ°№ӨЈ¬ЗуХв5ГыЦ°№ӨЦРЦБЙЩУР4ИЛөГ·ЦІ»ЙЩУЪ20·ЦөДёЕВКЈ»
ЈЁ2Ј©ТСЦӘФЪІвКФЦРЈ¬ІвКФДС¶ИөДјЖЛ㹫КҪОӘ![]() Ј¬ЖдЦР
Ј¬ЖдЦР![]() ОӘөЪ
ОӘөЪ![]() ПоІвКФДС¶ИЈ¬
ПоІвКФДС¶ИЈ¬![]() ОӘөЪ
ОӘөЪ![]() ПоәПёсөДИЛКэЈ¬
ПоәПёсөДИЛКэЈ¬![]() ОӘІОјУІвКФөДЧЬИЛКэ.ТСЦӘійИЎөДХв10ГыЦ°№ӨГҝПоІвКФәПёсИЛКэј°ПаУҰөДКөІвДС¶ИИзПВұнЈЁұн2Ј©Јә
ОӘІОјУІвКФөДЧЬИЛКэ.ТСЦӘійИЎөДХв10ГыЦ°№ӨГҝПоІвКФәПёсИЛКэј°ПаУҰөДКөІвДС¶ИИзПВұнЈЁұн2Ј©Јә
ұн2Јә
ІвКФПоДҝ | 1 | 2 | 3 | 4 | 5 |
КөІвәПёсИЛКэ | 8 | 8 | 7 | 7 | 2 |
¶ЁТеНіјЖБҝ![]() Ј¬ЖдЦР
Ј¬ЖдЦР![]() ОӘөЪ
ОӘөЪ![]() ПоөДКөІвДС¶ИЈ¬
ПоөДКөІвДС¶ИЈ¬![]() ОӘөЪ
ОӘөЪ![]() ПоөДФӨІвДС¶ИЈЁ
ПоөДФӨІвДС¶ИЈЁ![]() Ј©.№ж¶ЁЈәИф
Ј©.№ж¶ЁЈәИф![]() Ј¬ФтіЖёГҙОІвКФөДДС¶ИФӨІвәПАнЈ¬·сФтОӘІ»әПАнЈ¬ІвКФЗ°Ј¬ФӨ№АБЛГҝёцФӨІвПоДҝөДДС¶ИЈ¬ИзПВұнЈЁұн3Ј©ЛщКҫЈә
Ј¬ФтіЖёГҙОІвКФөДДС¶ИФӨІвәПАнЈ¬·сФтОӘІ»әПАнЈ¬ІвКФЗ°Ј¬ФӨ№АБЛГҝёцФӨІвПоДҝөДДС¶ИЈ¬ИзПВұнЈЁұн3Ј©ЛщКҫЈә
ұн3Јә
ІвКФПоДҝ | 1 | 2 | 3 | 4 | 5 |
ФӨІвЗ°ФӨ№АДС¶И | 0.9 | 0.8 | 0.7 | 0.6 | 0.4 |
ЕР¶ПұҫҙОІвКФөДДС¶ИФӨ№АКЗ·сәПАн.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ[СЎРЮ4-4ЈәЧшұкПөУлІОКэ·ҪіМ]
ФЪЖҪГжЦұҪЗЧшұкПө![]() ЦРЈ¬ЦұПЯ
ЦРЈ¬ЦұПЯ![]() өДІОКэ·ҪіМОӘ
өДІОКэ·ҪіМОӘ ЈЁ
ЈЁ![]() ОӘІОКэЈ©Ј¬ТФЧшұкФӯөгОӘј«өгЈ¬
ОӘІОКэЈ©Ј¬ТФЧшұкФӯөгОӘј«өгЈ¬![]() ЦбөД·Зёә°лЦбОӘј«ЦбЈ¬ҪЁБўј«ЧшұкПөЈ¬ЗъПЯ
ЦбөД·Зёә°лЦбОӘј«ЦбЈ¬ҪЁБўј«ЧшұкПөЈ¬ЗъПЯ![]() өДј«Чшұк·ҪіМОӘ
өДј«Чшұк·ҪіМОӘ![]() Ј®
Ј®
ЈЁ1Ј©ЗуЦұПЯ![]() өДЖХНЁ·ҪіМј°ЗъПЯ
өДЖХНЁ·ҪіМј°ЗъПЯ![]() өДЦұҪЗЧшұк·ҪіМЈ»
өДЦұҪЗЧшұк·ҪіМЈ»
ЈЁ2Ј©Йиөг![]() Ј¬ЦұПЯ
Ј¬ЦұПЯ![]() УлЗъПЯ
УлЗъПЯ![]() ПаҪ»УЪБҪөг
ПаҪ»УЪБҪөг![]() Ј¬
Ј¬![]() Ј¬Зу
Ј¬Зу![]() өДЦөЈ®
өДЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЈ¬¶аГжМе![]() ЦРЈ¬ЛДұЯРО
ЦРЈ¬ЛДұЯРО![]() ОӘҫШРОЈ¬¶юГжҪЗ
ОӘҫШРОЈ¬¶юГжҪЗ![]() ОӘ
ОӘ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() .
.

ЈЁ1Ј©ЗуЦӨЈә![]() ЖҪГж
ЖҪГж![]() Ј»
Ј»
ЈЁ2Ј©![]() ОӘПЯ¶О
ОӘПЯ¶О![]() ЙПөДөгЈ¬өұ
ЙПөДөгЈ¬өұ![]() КұЈ¬Зу¶юГжҪЗ
КұЈ¬Зу¶юГжҪЗ![]() өДУаПТЦө.
өДУаПТЦө.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЦұҪЗЧшұкПөЦРЈ¬ФІ![]() Јә
Јә![]() ҫӯ№эЙмЛхұд»»
ҫӯ№эЙмЛхұд»»![]() Ј¬әуөГөҪЗъПЯ
Ј¬әуөГөҪЗъПЯ![]() ТФЧшұкФӯөгОӘј«өгЈ¬xЦбөДХэ°лЦбОӘј«ЦбЈ¬ІўФЪБҪЦЦЧшұкПөЦРИЎПаН¬өДөҘО»іӨ¶ИЈ¬ҪЁБўј«ЧшұкПөЈ¬ЦұПЯlөДј«Чшұк·ҪіМОӘ
ТФЧшұкФӯөгОӘј«өгЈ¬xЦбөДХэ°лЦбОӘј«ЦбЈ¬ІўФЪБҪЦЦЧшұкПөЦРИЎПаН¬өДөҘО»іӨ¶ИЈ¬ҪЁБўј«ЧшұкПөЈ¬ЦұПЯlөДј«Чшұк·ҪіМОӘ![]()
![]() ЗуЗъПЯ
ЗуЗъПЯ![]() өДЦұҪЗЧшұк·ҪіМј°ЦұПЯlөДЦұҪЗЧшұк·ҪіМЈ»
өДЦұҪЗЧшұк·ҪіМј°ЦұПЯlөДЦұҪЗЧшұк·ҪіМЈ»
![]() ФЪ
ФЪ![]() ЙПЗуТ»өгMЈ¬К№өгMөҪЦұПЯlөДҫаАлЧоРЎЈ¬ІўЗуіцЧоРЎҫаАлЈ®
ЙПЗуТ»өгMЈ¬К№өгMөҪЦұПЯlөДҫаАлЧоРЎЈ¬ІўЗуіцЧоРЎҫаАлЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФІЧ¶![]() ЈЁЖдЦР
ЈЁЖдЦР![]() ОӘ¶ҘөгЈ¬
ОӘ¶ҘөгЈ¬![]() ОӘөЧГжФІРДЈ©өДІаГж»эУлөЧГж»эөДұИКЗ
ОӘөЧГжФІРДЈ©өДІаГж»эУлөЧГж»эөДұИКЗ![]() Ј¬ФтФІЧ¶
Ј¬ФтФІЧ¶![]() УлЛьНвҪУЗтЈЁјҙ¶ҘөгФЪЗтГжЙПЗТөЧГжФІЦЬТІФЪЗтГжЙПЈ©өДМе»эұИОӘЈЁ Ј©
УлЛьНвҪУЗтЈЁјҙ¶ҘөгФЪЗтГжЙПЗТөЧГжФІЦЬТІФЪЗтГжЙПЈ©өДМе»эұИОӘЈЁ Ј©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝЙиaЎКRЈ¬КэБР{an}ВъЧгa1ЈҪaЈ¬an+1ЈҪan©ҒЈЁan©Ғ2Ј©3Ј¬ФтЈЁЎЎЎЎЈ©
A.өұaЈҪ4КұЈ¬a10Јҫ210B.өұ![]() КұЈ¬a10Јҫ2
КұЈ¬a10Јҫ2
C.өұ![]() КұЈ¬a10Јҫ210D.өұ
КұЈ¬a10Јҫ210D.өұ![]() КұЈ¬a10Јҫ2
КұЈ¬a10Јҫ2
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘДіёЯРЈЧЫәПЖАјЫУРБҪІҪЈәөЪТ»ІҪКЗІДБПіхЙуЈ¬ИфІДБПіхЙуІ»әПёсЈ¬ФтІ»ДЬҪшИлөЪ¶юІҪГжКФЈ»ИфІДБПіхЙуәПёсЈ¬ФтҪшИлөЪ¶юІҪГжКФ.Ц»УРГжКФәПёсХЯЈ¬ІЕДЬ»сөГёГёЯРЈЧЫәПЖАјЫөДВјИЎЧКёсЈ¬ПЦУРAЈ¬BЈ¬CИэГыС§ЙъұЁГыІОјУёГёЯРЈөДЧЫәПЖАјЫЈ¬јЩЙиAЈ¬BЈ¬CИэО»С§ЙъІДБПіхЙуәПёсөДёЕВК·ЦұрКЗ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј»ГжКФәПёсөДёЕВК·ЦұрКЗ
Ј»ГжКФәПёсөДёЕВК·ЦұрКЗ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() .
.
ЈЁ1Ј©ЗуAЈ¬BБҪО»ҝјЙъУРЗТЦ»УРТ»О»ҝјЙъ»сөГВјИЎЧКёсөДёЕВКЈ»
ЈЁ2Ј©јЗЛж»ъұдБҝXОӘAЈ¬BЈ¬CИэО»С§Йъ»сөГёГёЯРЈЧЫәПЖАјЫВјИЎЧКёсөДИЛКэЈ¬ЗуXөДёЕВК·ЦІјУлКэС§ЖЪНы.
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com