
【题目】某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品.现用两种新配方(分别称为A配方和B配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
A配方的频数分布表
指标值分组 | [90,94) | [94,98) | [98,102) | [102,106) | [106,110] |
频数 | 8 | 20 | 42 | 22 | 8 |
B配方的频数分布表
指标值分组 | [90,94) | [94,98) | [98,102) | [102,106) | [106,110] |
频数 | 4 | 12 | 42 | 32 | 10 |
(1)分别估计用A配方,B配方生产的产品的优质品率;
(2)已知用B配方生产的一件产品的利润y(单位:元)与其质量指标值t的关系式为y= 
估计用B配方生产的一件产品的利润大于0的概率,并求用B配方生产的上述100件产品平均一件的利润.
【答案】
(1)解:由试验结果知,用A配方生产的产品中优质品的频率为 ![]() =0.3,
=0.3,
所以用A配方生产的产品的优质品率的估计值为0.3.
由试验结果知,用B配方生产的产品中优质品的频率为 ![]() =0.42,
=0.42,
所以用B配方生产的产品的优质品率的估计值为0.42
(2)解:由条件知,用B配方生产的一件产品的利润大于0,当且仅当其质量指标值t≥94.
由试验结果知,质量指标值t≥94的频率为0.96.
所以用B配方生产的一件产品的利润大于0的概率估计值为0.96.
用B配方生产的产品平均一件的利润为
![]() ×[4×(﹣2)+54×2+42×4]=2.68(元)
×[4×(﹣2)+54×2+42×4]=2.68(元)
【解析】(1)由试验结果先求出用A配方生产的产品中优质品的频率和用B配方生产的产品中优质品的频率,由此能分别估计用A配方,B配方生产的产品的优质品率.(2)由条件知,用B配方生产的一件产品的利润大于0,当且仅当其质量指标值t≥94.由试验结果知,质量指标值t≥94的频率为0.96.由此能求出用B配方生产的产品平均一件的利润.


科目:高中数学 来源: 题型:
【题目】已知 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),其中0<α<β<π.
=(cosβ,sinβ),其中0<α<β<π.
(1)求证: ![]() 与
与 ![]() 互相垂直;
互相垂直;
(2)若k ![]() 与
与 ![]() ﹣k
﹣k ![]() 的长度相等,求β﹣α的值(k为非零的常数).
的长度相等,求β﹣α的值(k为非零的常数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某军工企业生产一种精密电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数:R(x)= 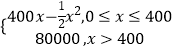 其中x是仪器的月产量.
其中x是仪器的月产量.
(1)将利润表示为月产量的函数;
(2)当月产量为何值时,公司所获利润最大?最大利润是多少元?(总收益=总成本+利润.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(0,3),直线l:y=2x﹣4.设圆C的半径为1,圆心在l上.
(1)若圆心C也在直线y=x﹣1上,过点A作圆C的切线,求切线的方程;
(2)若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正四棱锥S﹣ABCD中,E,M,N分别是BC,CD,SC的中点,动点P在线段MN上运动时,下列四个结论:①EP⊥AC;②EP∥BD;③EP∥面SBD;④EP⊥面SAC.中恒成立的为( ) 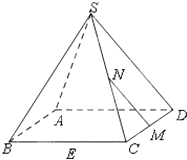
A.①③
B.③④
C.①②
D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人各自独立地进行射击比赛,甲、乙两人各射击一次,击中目标的概率分别是 ![]() 和
和 ![]() ,假设每次射击是否击中目标相互之间没有影响.
,假设每次射击是否击中目标相互之间没有影响.
(1)求甲射击3次,至少有1次未击中目标的概率;
(2)求两人各射击3次,甲恰好击中目标2次且乙恰好击中目标1次的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com