
【题目】已知 ![]() =(cosα,sinα),
=(cosα,sinα), ![]() =(cosβ,sinβ),其中0<α<β<π.
=(cosβ,sinβ),其中0<α<β<π.
(1)求证: ![]() 与
与 ![]() 互相垂直;
互相垂直;
(2)若k ![]() 与
与 ![]() ﹣k
﹣k ![]() 的长度相等,求β﹣α的值(k为非零的常数).
的长度相等,求β﹣α的值(k为非零的常数).
【答案】
(1)证明:由题意得: ![]() +
+ ![]() =(cosα+cosβ,sinα+sinβ)
=(cosα+cosβ,sinα+sinβ)
![]() ﹣
﹣ ![]() =(cosα﹣cosβ,sinα﹣sinβ)
=(cosα﹣cosβ,sinα﹣sinβ)
∴( ![]() +
+ ![]() )(
)( ![]() ﹣
﹣ ![]() )=(cosα+cosβ)(cosα﹣cosβ)+(sinα+sinβ)(sinα﹣sinβ)
)=(cosα+cosβ)(cosα﹣cosβ)+(sinα+sinβ)(sinα﹣sinβ)
=cos2α﹣cos2β+sin2α﹣sin2β=1﹣1=0
∴ ![]() +
+ ![]() 与
与 ![]() ﹣
﹣ ![]() 互相垂直
互相垂直
(2)证明:解:方法一:k ![]() +
+ ![]() =(kcosα+cosβ,ksinα+sinβ),
=(kcosα+cosβ,ksinα+sinβ),
![]() ﹣k
﹣k ![]() =(cosα﹣kcosβ,sinα﹣ksinβ)
=(cosα﹣kcosβ,sinα﹣ksinβ)
|k ![]() +
+ ![]() |=
|= ![]() ,|
,| ![]() ﹣k
﹣k ![]() |=
|= ![]()
由题意,得4cos(β﹣α)=0,
因为0<α<β<π,
所以β﹣α= ![]() .
.
方法二:由|k ![]() +
+ ![]() |=|
|=| ![]() ﹣k
﹣k ![]() |得:|k
|得:|k ![]() +
+ ![]() |2=|
|2=| ![]() ﹣k
﹣k ![]() |2
|2
即(k ![]() +
+ ![]() )2=(
)2=( ![]() ﹣k
﹣k ![]() )2,k2|
)2,k2| ![]() |2+2k
|2+2k ![]()
![]() +|
+| ![]() |2=|
|2=| ![]() |2﹣2k
|2﹣2k ![]()
![]() +k2|
+k2| ![]() |2
|2
由于| ![]() |=1,|
|=1,| ![]() |=1
|=1
∴k2+2k ![]()
![]() +1=1﹣2k
+1=1﹣2k ![]()
![]() +k2,故
+k2,故 ![]()
![]() =0,
=0,
即(cosα,sinα)(cosβ,sinβ)=0(10分)
即cosαcosβ+sinαsnβ=4cos (β﹣α)=0
因为0<α<β<π,
所以β﹣α= ![]()
【解析】(1)根据已知中向量 ![]() ,
, ![]() 的坐标,分别求出向量
的坐标,分别求出向量 ![]() +
+ ![]() 与
与 ![]() ﹣
﹣ ![]() 的坐标,进而根据向量数量积公式及同角三角函数的平方关系,可证得
的坐标,进而根据向量数量积公式及同角三角函数的平方关系,可证得 ![]() 与
与 ![]() 互相垂直;(2)方法一:分别求出k
互相垂直;(2)方法一:分别求出k ![]() 与
与 ![]() ﹣k
﹣k ![]() 的坐标,代入向量模的公式,求出k
的坐标,代入向量模的公式,求出k ![]() 与
与 ![]() ﹣k
﹣k ![]() 的模,进而可得cos(β﹣α)=0,结合已知中0<α<β<π,可得答案. 方法二:由|k
的模,进而可得cos(β﹣α)=0,结合已知中0<α<β<π,可得答案. 方法二:由|k ![]() +
+ ![]() |=|
|=| ![]() ﹣k
﹣k ![]() |得:|k
|得:|k ![]() +
+ ![]() |2=|
|2=| ![]() ﹣k
﹣k ![]() |2 , 即(k
|2 , 即(k ![]() +
+ ![]() )2=(
)2=( ![]() ﹣k
﹣k ![]() )2 , 展开后根据两角差的余弦公式,可得cos(β﹣α)=0,结合已知中0<α<β<π,可得答案.
)2 , 展开后根据两角差的余弦公式,可得cos(β﹣α)=0,结合已知中0<α<β<π,可得答案.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:
【题目】下列四组函数中,表示同一函数的是( )
A.f(x)=|x|,g(x)= ![]()
B.f(x)=lg x2 , g(x)=2lg x
C.f(x)= ![]() ,g(x)=x+1
,g(x)=x+1
D.f(x)= ![]() ?
? ![]() ,g(x)=
,g(x)= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学名著《九章算术》中有这样一个问题:今有牛、马、羊食人苗,苗主责之粟五斗,羊主曰:“我羊食半马.”马主曰:“我马食半牛.”今欲衰偿之,问各出几何?此问题的译文是:今有牛、马、羊吃了别人的禾苗,禾苗主人要求赔偿5斗粟.羊主人说:“我羊所吃的禾苗只有马的一半.”马主人说:“我马所吃的禾苗只有牛的一半.”打算按此比例偿还,他们各应偿还多少?已知牛、马、羊的主人各应偿还![]() 升,
升, ![]() 升,
升, ![]() 升,1斗为10升,则下列判断正确的是( )
升,1斗为10升,则下列判断正确的是( )
A. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
B. ![]() ,
, ![]() ,
, ![]() 依次成公比为2的等比数列,且
依次成公比为2的等比数列,且![]()
C. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
D. ![]() ,
, ![]() ,
, ![]() 依次成公比为
依次成公比为![]() 的等比数列,且
的等比数列,且![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交BC于点E,AB=2AC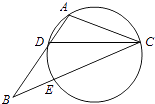
(1)求证:BE=2AD;
(2)当AC=3,EC=6时,求AD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正四棱锥![]() 中,已知异面直线
中,已知异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ,给出下面三个命题:
,给出下面三个命题:
![]() :若
:若![]() ,则此四棱锥的侧面积为
,则此四棱锥的侧面积为![]() ;
;
![]() :若
:若![]() 分别为
分别为![]() 的中点,则
的中点,则![]() 平面
平面![]() ;
;
![]() :若
:若![]() 都在球
都在球![]() 的表面上,则球
的表面上,则球![]() 的表面积是四边形
的表面积是四边形![]() 面积的
面积的![]() 倍.
倍.
在下列命题中,为真命题的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用0,1,2,3,4,5这六个数字:
(1)能组成多少个无重复数字的四位偶数?
(2)能组成多少个无重复数字且为5的倍数的五位数?
(3)能组成多少个无重复数字且比1325大的四位数?(以上各问均用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品.现用两种新配方(分别称为A配方和B配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
A配方的频数分布表
指标值分组 | [90,94) | [94,98) | [98,102) | [102,106) | [106,110] |
频数 | 8 | 20 | 42 | 22 | 8 |
B配方的频数分布表
指标值分组 | [90,94) | [94,98) | [98,102) | [102,106) | [106,110] |
频数 | 4 | 12 | 42 | 32 | 10 |
(1)分别估计用A配方,B配方生产的产品的优质品率;
(2)已知用B配方生产的一件产品的利润y(单位:元)与其质量指标值t的关系式为y= 
估计用B配方生产的一件产品的利润大于0的概率,并求用B配方生产的上述100件产品平均一件的利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com