
【题目】已知![]() ,其中常数
,其中常数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的极值;
的极值;
(2)若函数![]() 有两个零点
有两个零点![]() ,求证:
,求证: ![]() ;
;
(3)求证: ![]() .
.
选做题:
【答案】(1) ![]() 有极小值
有极小值![]() ,没有极大值.(2)证明见解析;(3)证明见解析.
,没有极大值.(2)证明见解析;(3)证明见解析.
【解析】试题分析:先写出函数![]() 的定义域,(1)由
的定义域,(1)由![]() ,求出
,求出![]() 的导数,再求出
的导数,再求出![]() 的单调性,即可求得极值;(2)先证明:当
的单调性,即可求得极值;(2)先证明:当![]() 恒成立时,有
恒成立时,有![]() 成立,若
成立,若![]() ,则
,则![]() 显然成立;若
显然成立;若![]() ,运用参数分离,构造新函数通过求导数及单调性,结合函数零点存在定理,即可得证;(3)讨论当当
,运用参数分离,构造新函数通过求导数及单调性,结合函数零点存在定理,即可得证;(3)讨论当当![]() 时,
时, ![]() 恒成立,可设设
恒成立,可设设![]() ,求出导数,单调区间及最大值,运用不等式的性质,即可得证.
,求出导数,单调区间及最大值,运用不等式的性质,即可得证.
试题解析:函数![]() 的定义域为
的定义域为![]() ,
,
(1)当![]() 时,
时, ![]() ,
, ![]() ,
,
而![]() 在
在![]() 上单调递增,又
上单调递增,又![]() ,
,
当![]() 时,
时, ![]() ,则
,则![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时, ![]() ,则
,则![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() 有极小值
有极小值![]() ,没有极大值.
,没有极大值.
(2)先证明:当![]() 恒成立时,有
恒成立时,有![]() 成立.
成立.
若![]() ,则
,则![]() 显然成立;
显然成立;
若![]() ,由
,由![]() 得
得![]() ,令
,令![]() ,
,
则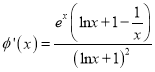 ,
,
令![]() ,由
,由![]() 得
得![]() 在
在![]() 上单调递增,
上单调递增,
又∵![]() ,所以
,所以![]() 在
在![]() 上为负,在
上为负,在![]() 上为正,
上为正,
∴![]() 在
在![]() 上递减,在
上递减,在![]() 上递增
上递增
∴![]() ,从而
,从而![]() .
.
因而函数![]() 若有两个零点,则
若有两个零点,则![]() ,所以
,所以![]() ,
,
由![]() 得
得![]() ,则
,则
![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,
,
∴![]() 在
在![]() 上单调递增
上单调递增
∴![]() ,则
,则![]()
∴![]()
由![]() 得
得![]() ,则
,则![]()
∴![]() ,
,
综上得![]() .
.
(3)由(2)知当![]() 时,
时, ![]() 恒成立,所以
恒成立,所以![]() ,
,
即![]() ,
,
设![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递减;
上单调递减;
所以![]() 的最大值为
的最大值为![]() ,即
,即![]() ,
,
因而![]() ,
,
所以![]() ,即
,即![]()
点睛:导数是研究函数的单调性、极值(最值)最有效的工具对导数的应用的考查主要从以下几个角度进行:(1)考查导数的几何意义,往往与解析几何、微积分相联系;(2)利用导数求函数的单调区间,判断单调性;已知单调性求参数;(3)利用导数求函数的最值(极值),解决生活中的优化问题;(4)考查数形结合思想的应用.


科目:高中数学 来源: 题型:
【题目】共享单车的推广给消费者带来全新消费体验,迅速赢得广大消费者的青睐,然而,同时也暴露出管理、停放、服务等方面的问题,为了了解公众对共享单车的态度(提倡或不提倡),某调查小组随机地对不同年龄段50人进行调查,将调查情况整理如下表:

并且,年龄在![]() 和
和![]() 的人中持“提倡”态度的人数分别为5和3,现从这两个年龄段中随机抽取2人征求意见.
的人中持“提倡”态度的人数分别为5和3,现从这两个年龄段中随机抽取2人征求意见.
(Ⅰ)求年龄在![]() 中被抽到的2人都持“提倡”态度的概率;
中被抽到的2人都持“提倡”态度的概率;
(Ⅱ)求年龄在![]() 中被抽到的2人至少1人持“提倡”态度的概率.
中被抽到的2人至少1人持“提倡”态度的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市根据地理位置划分成了南北两区,为调查该市的一种经济作物![]() (下简称
(下简称![]() 作物)的生长状况,用简单随机抽样方法从该市调查了 500 处
作物)的生长状况,用简单随机抽样方法从该市调查了 500 处 ![]() 作物种植点,其生长状况如表:
作物种植点,其生长状况如表:

其中生长指数的含义是:2 代表“生长良好”,1 代表“生长基本良好”,0 代表“不良好,但仍有收成”,﹣1代表“不良好,绝收”.
(1)估计该市空气质量差的![]() 作物种植点中,不绝收的种植点所占的比例;
作物种植点中,不绝收的种植点所占的比例;
(2)能否有 99%的把握认为“该市![]() 作物的种植点是否绝收与所在地域有关”?
作物的种植点是否绝收与所在地域有关”?
(3)根据(2)的结论,能否提供更好的调查方法来估计该市![]() 作物的种植点中,绝收种植点的比例?请说明理由.
作物的种植点中,绝收种植点的比例?请说明理由.


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 为梯形,
为梯形,![]() ,
,![]() ,且
,且![]() .
.

(Ⅰ)若点![]() 为
为![]() 上一点且
上一点且![]() ,证明:
,证明:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的标准方程为
的标准方程为![]() ,离心率
,离心率![]() ,且椭圆经过点
,且椭圆经过点![]() .过右焦点
.过右焦点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的方程.
的方程.
(Ⅱ)若![]() ,求直线
,求直线![]() 的方程.
的方程.
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得以
,使得以![]() ,
, ![]() 为邻边的四边形
为邻边的四边形![]() 是菱形,且点
是菱形,且点![]() 在椭圆上.若存在,求出
在椭圆上.若存在,求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com