
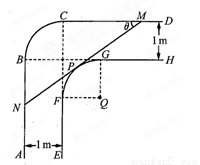
一走廊拐角处的横截面如图所示,已知内壁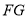 和外壁
和外壁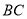 都是半径为1m的四分之一圆弧,
都是半径为1m的四分之一圆弧,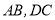 分别与圆弧
分别与圆弧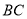 相切于
相切于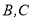 两点,
两点, 且两组平行墙壁间的走廊宽度都是1m.
且两组平行墙壁间的走廊宽度都是1m.
(1)若水平放置的木棒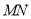 的两个端点
的两个端点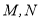 分别在外壁
分别在外壁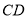 和
和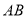 上,且木棒与内壁圆弧相切于点
上,且木棒与内壁圆弧相切于点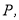 设
设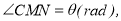 试用
试用 表示木棒
表示木棒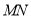 的长度
的长度
(2)若一根水平放置的木棒能通过该走廊拐角处,求木棒长度的最大值.
(1) ;(2)
;(2)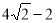 .
.
【解析】
试题分析:(1)如图,设圆弧FG所在的圆的圆心为Q,过Q点作CD垂线,垂足为点T,且交MN或其延长线与于S,并连接PQ,再过N点作TQ的垂线,垂足为W.在 中用NW和
中用NW和 表示出NS,在
表示出NS,在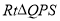 中用PQ和
中用PQ和 表示出QS,然后分别看S在线段TG上和在线段GT的延长线上分别表示出TS=QT-QS,然后在
表示出QS,然后分别看S在线段TG上和在线段GT的延长线上分别表示出TS=QT-QS,然后在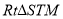 中表示出MS,利用MN=NS+MS求得MN的表达式和
中表示出MS,利用MN=NS+MS求得MN的表达式和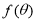 的表达式.
的表达式.
(2)设出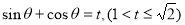 ,则
,则 可用t表示出,然后可得
可用t表示出,然后可得 关于t的表达式,对函数进行求导,根据t的范围判断出导函数与0的大小,进而就可推断出函数的单调性;然后根据t的范围求得函数的最小值.
关于t的表达式,对函数进行求导,根据t的范围判断出导函数与0的大小,进而就可推断出函数的单调性;然后根据t的范围求得函数的最小值.
试题解析:⑴如图,设圆弧FG所在的圆的圆心为Q,过Q点作CD的垂线,垂足为点T,且交MN或其延长线于S,并连结PQ,再过点N作TQ的垂线,垂足为W,在 中,因为NW=2,
中,因为NW=2, ,所以
,所以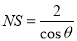 ,因为MN与圆弧FG切于点P,所以
,因为MN与圆弧FG切于点P,所以 ,在
,在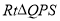 中,因为PQ=1,
中,因为PQ=1,
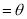 ,所以
,所以 ,
,
①若M在线段TD上,即S在线段TG上,则TS=QT-QS,
在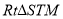 中,
中, ,
,
因此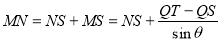 .
.
②若M在线段CT上,即若S在线段GT的延长线上,则TS=QS-QT,
在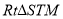 中,
中,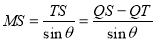 ,
,
因此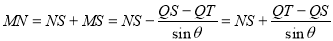 .
.
 .
.
(2)设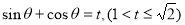 ,则
,则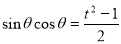 ,
,
因此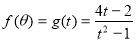 .因为
.因为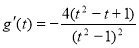 ,又
,又 ,所以
,所以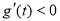 恒成立,
恒成立,
因此函数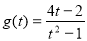 在
在 是减函数,所以
是减函数,所以
即 .
.
所以一根水平放置的木棒若能通过该走廊拐角处,则其长度的最大值为 .
.
考点:解三角形的实际应用.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源:2015届江苏省扬州市高二下学期期末考试文科数学试卷(解析版) 题型:填空题
“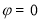 ”是“函数
”是“函数 为奇函数”的 条件.
为奇函数”的 条件.
(从“充要”,“充分不必要”,“必要不充分”,“既不充分也不必要”中选择适当的填写)
查看答案和解析>>
科目:高中数学 来源:2015届江苏省高二下学期月考数学试卷(解析版) 题型:解答题
甲、乙、丙三名音乐爱好者参加某电视台举办的演唱技能海选活动,在本次海选中有合格和不合格两个等级.若海选合格记 分,海选不合格记
分,海选不合格记 分.假设甲、乙、丙海选合格的概率分别为
分.假设甲、乙、丙海选合格的概率分别为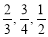 ,他们海选合格与不合格是相互独立的.
,他们海选合格与不合格是相互独立的.
(1)求在这次海选中,这三名音乐爱好者至少有一名海选合格的概率;
(2)记在这次海选中,甲、乙、丙三名音乐爱好者所得分之和为随机变量 ,求随机变量
,求随机变量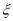 的分布列和数学期望
的分布列和数学期望 .
.
查看答案和解析>>
科目:高中数学 来源:2015届江苏省高三8月开学考试数学试卷(解析版) 题型:解答题
抛掷A,B,C三枚质地不均匀的纪念币,它们正面向上的概率如下表所示 ;
;
纪念币 | A | B | C |
概率 |
| a | a |
将这三枚纪念币同时抛掷一次,设 表示出现正面向上的纪念币的个数.
表示出现正面向上的纪念币的个数.
(1)求 的分布列及数学期望;
的分布列及数学期望;
(2)在概率 中,若
中,若 的值最大,求a的最大值
的值最大,求a的最大值
查看答案和解析>>
科目:高中数学 来源:2015届江苏省高三8月开学考试数学试卷(解析版) 题型:填空题
下列说法中,正确的有 .(写出所有正确命题的序号).
①若f?(x0)=0,则f(x0)为f(x)的极值点;
②在闭区间[a,b]上,极大值中最大的就是最大值;
③若f(x)的极大值为f(x1),f(x)的极小值为f(x2),则f(x1)>f(x2);
④有的函数有可能有两个最小值;
⑤已知函数 ,对于
,对于 定义域内的任意一个
定义域内的任意一个 都存在唯一个
都存在唯一个 成立.
成立.
查看答案和解析>>
科目:高中数学 来源:2015届江苏省南京市高三9月调研考试理科数学试卷(解析版) 题型:解答题
已知函数f(x)=2sin(2x+φ)(0<φ<2π)的图象过点( ,-2).
,-2).
(1)求φ的值;
(2)若f( )=
)= ,-
,- <α<0,求sin(2α-
<α<0,求sin(2α- )的值.
)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com