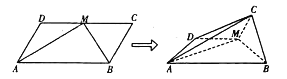
【题目】如图，平行四边形
中，
，
，
为
边的中点，沿
将
折起使得平面
平面
.
（1）求证：平面
平面
；
（2）求四棱锥
的体积；
（3）求折后直线
与平面
所成的角的正弦值.
【答案】（1）证明见解析（2）
（3）
【解析】
（1）根据面面垂直的性质定理，证得
平面
，由此证得平面
平面.
（2）
的中点
，根据等比三角形的性质得到
由面面垂直的性质定理得
平面
，也即
是四棱锥
的高.进而求得四棱锥的体积.
（3）以
为空间坐标系原点建立空间直角坐标系，利用直线
的方向向量和平面
的法向量，计算出直线与平面所成的角的正弦值.
（1）证明：∵平面
平面，平面
平面
，
由题易知
，且
平面.
∴平面，而平面
，
∴平面平面.
（2）由已知有
是正三角形，取的中点，则，又平面平面于，
则平面，且
，
易求得
，
∴
.
（3）作
，由（1）知可如图建系，
则
，
，
，
，
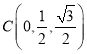又
，得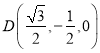
，
，
.
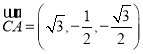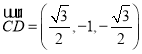设平面
的法向量
，则
，不妨取
.
设折后直线与平面所成的角为
，则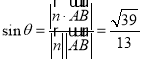
.
科目：高中数学 来源： 题型：
【题目】某高新企业自2012年成立以来，不断创新技术与产品，积极拓展市场，销售收入
（单位万元）与年份代号
之间对应关系如下表，且满足回归函数
，记
。
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售收入 | 80 | 199 | 398 | 2512 | 6310 | 15848 | 79432 |
| 1.9 | 2.3 | 2.6 | 3.4 | 3.8 | 4.2 | 4.9 |
（1）任取2年对比销售收入的情况，求这2年中销售收入均超过400万元的概率；
（2）求回归函数中
的值。
附：对于一组数据
，其回归直线
的斜率和截距的最小二乘估计分别为
，
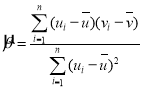查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一幢高楼上安放了一块高约10 米的 LED 广告屏，一测量爱好者在与高楼底部同一水平线上的 C 处测得广告屏顶端A 处的仰角为 31.80°，再向大楼前进 20 米到 D 处，测得广告屏顶端 A 处的仰角为 37.38°（人的高度忽略不计）．
（1）求大楼的高度（从地面到广告屏顶端）（精确到 1 米）；
（2）若大楼的前方是一片公园空地，空地上可以安放一些长椅，为使坐在其中一个长椅上观看广告屏最清晰（长 椅的高度忽略不计），长椅需安置在距大楼底部 E 处多远？已知视角 ∠AMB（ M 为观测者的位置， B 为广告屏 底部）越大，观看得越清晰．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在三棱锥
中，OA、OB、OC所在直线两两垂直，且
，CA与平面AOB所成角为
，D是AB中点，三棱锥的体积是
．
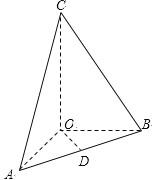
（1）求三棱锥的高；
（2）在线段CA上取一点E，当E在什么位置时，异面直线BE与OD所成的角为
？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，三棱柱
中，
侧面
，已知
，
，
，点
是棱
的中点.
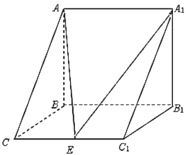
（1）求证：
平面
；
（2）求二面角
的余弦值；
（3）在棱
上是否存在一点
，使得
与平面
所成角的正弦值为
，若存在，求出
的值；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】平面内任意一点
到两定点
、
的距离之和为
.
（1）若点是第二象限内的一点且满足
，求点的坐标；
（2）设平面内有关于原点对称的两定点
，判别
是否有最大值和最小值，请说明理由？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
