
����Ŀ��ij��������ͬ���Ĵ�λ100�ţ����ݾ��飬���ñ��ݵĴ��ۣ���ÿ�Ŵ�ÿ�����𣩲�����10Ԫʱ����λ����ȫ������������۸���10Ԫʱ��ÿ���1Ԫ������3�Ŵ�λ���У�Ϊ�˻�ýϺõ�Ч�棬�ñ���Ҫ����λ��һ�����ʵļ۸������ǣ���Ҫ������ˣ�����ӦΪ1Ԫ��������;���ñ���ÿ�յķ���֧��Ϊ575Ԫ����λ���������������֧�������Ҹ߳���Խ��Խ�ã�����x��ʾ���ۣ���y��ʾ�ñ���һ����ⴲλ�ľ����루����ȥÿ�յķ���֧��������룩��
��1����y��ʾ��x�ĺ�����������䶨����;
��2����ȷ���ñ��ݽ���λ����Ϊ����ʱ���ȷ����������������������ʹ���������?
���𰸡���1������y= ![]() ��������Ϊ{x|
��������Ϊ{x|![]()
![]() }��
}��
��2������λ����Ϊ22Ԫʱ��������࣮
��������
�����������1����������������ȥ֧�������������Ϊ![]() ��
��![]() ������������ʽ��ͬʱע�⾻�������������Ҽ۸�Ϊ�����������Զ�ÿ�κ����Ķ��������ϸ����ƣ���2���ɷֶκ������ص㣬������κ����ֱ������ֵ�������������Ǹ����ֵ��Ϊ����
������������ʽ��ͬʱע�⾻�������������Ҽ۸�Ϊ�����������Զ�ÿ�κ����Ķ��������ϸ����ƣ���2���ɷֶκ������ص㣬������κ����ֱ������ֵ�������������Ǹ����ֵ��Ϊ����
��������� ��1����������
y= ![]()
![]() ��
��![]()
![]() ��
��
��Ϊ![]()
![]() ��
��
�� ![]() ��
��![]()
![]() ��
��
�� ![]() ��
��![]()
![]()
![]() ��
��
���Ժ���Ϊ
y= ![]()
������Ϊ{x|![]()
![]() }��
}��
��2����x=10ʱ![]()
![]() ��ȡ�����ֵ425Ԫ��
��ȡ�����ֵ425Ԫ��
��x��10ʱ![]()
���ҽ���![]() ʱ��yȡ���ֵ��
ʱ��yȡ���ֵ��
��![]()
![]() �����Ե�x=22ʱ
�����Ե�x=22ʱ![]()
![]() ��ȡ�����ֵ833Ԫ���Ƚ������������֪����λ����Ϊ22Ԫʱ��������࣮
��ȡ�����ֵ833Ԫ���Ƚ������������֪����λ����Ϊ22Ԫʱ��������࣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y=f ��x��= ![]() ��
��
��1������f ��x����ͼ����x= ![]() �������߷��̣�
�������߷��̣�
��2����y=f��x�������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���С���Ԫ�����̹���ë��ѭ������������������������ֻ����һ�������и�һ���߶��������������Ӳ�������һʤ�߶��ĸ���Ϊ![]() ����һʤ�����ĸ���Ϊ
����һʤ�����ĸ���Ϊ![]() ���߶�ʤ�����ĸ���Ϊ
���߶�ʤ�����ĸ���Ϊ![]() ��ÿ��ʤ���������ʤ��1�֣�����0�֣��涨��������ͬʱ�����꼶��ʤ.
��ÿ��ʤ���������ʤ��1�֣�����0�֣��涨��������ͬʱ�����꼶��ʤ.
��1����������ùھ��ĸ���Ϊ![]() ����
����![]() ��
��
��2���Ǹ����ĵ÷�Ϊ![]() ����
����![]() �ķֲ��к�����.
�ķֲ��к�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x���Ķ�����Ϊ����2��2��������g��x��=f��x��1��+f��3��2x����
��1������g��x���Ķ�����
��2����f��x�����溯�����ڶ������ڵ����ݼ�����ʽg��x����0�Ľ⼯
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������12�֣���֪����{an}�ǵȲ����У���a1��a2��a1��a2���ֱ�Ϊ����x2��6x+5=0�Ķ�����
��1��������{an}��ǰn���Sn��
��2���ڣ�1���У���bn=![]() ����֤����c=��
����֤����c=��![]() ʱ������{bn}�ǵȲ����У�
ʱ������{bn}�ǵȲ����У�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����f��x��=1��![]() ,��⣺��1��f��x����ֵ��2��֤��f��x��ΪR�ϵ��������� ��
,��⣺��1��f��x����ֵ��2��֤��f��x��ΪR�ϵ��������� ��
��1����f��x����ֵ��
��2��֤��f��x��ΪR�ϵ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����˵��ϣ���ϴ����˹ѧ�ɵ���ѧ�Ҿ�����ɳ̲���滭�����Сʯ�ӱ�ʾ���������о�����ͼ��ʾ������������
����������1��3��6��10������Ϊ����{an}�����ɱ�5������������������С�����˳�����һ��������{bn}�������Ʋ⣺
��1��b5=��
��2��b2n��1= �� 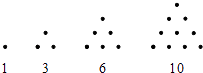
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����弯��A={x|2x��1}��B={y|y= ![]() }����A��RB=�� ��
}����A��RB=�� ��
A.��1��+�ޣ�
B.[0��1]
C.[0��1��
D.[1��+�ޣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com