
【题目】已知抛物线![]() 的顶点为原点
的顶点为原点![]() ,焦点为圆
,焦点为圆![]() 的圆心
的圆心![]() .经过点
.经过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点,交圆
两点,交圆![]() 于
于![]() 两点,
两点, ![]() 在第一象限,
在第一象限, ![]() 在第四象限.
在第四象限.
(1)求抛物线![]() 的方程;
的方程;
(2)是否存在直线![]() ,使
,使![]() 是
是![]() 与
与![]() 的等差中项?若存在,求直线
的等差中项?若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】试题分析:(1)根据圆的圆心为抛物线的焦点,可求得![]() ,即可求得抛物线方程
,即可求得抛物线方程![]() ;(2)若是等差中项,那么
;(2)若是等差中项,那么![]() ,那么
,那么![]() ,再根据抛物线的焦点弦长可知
,再根据抛物线的焦点弦长可知![]() ,将问题转化为根与系数的关系,求出直线方程.
,将问题转化为根与系数的关系,求出直线方程.
试题解析:(1)根据已知设抛物线![]() 的方程为
的方程为![]() .
.
∵圆![]() 的方程为
的方程为![]() ,
,
∴圆心![]() 的坐标为
的坐标为![]() ,半径
,半径![]() .
.
∴![]() ,解得
,解得![]() .
.
∴抛物线![]() 的方程为
的方程为![]() .
.
(2)∵![]() 是
是![]() 与
与![]() 的等差中项,∴
的等差中项,∴![]() .
.
∴![]() .
.
若![]() 垂直于
垂直于![]() 轴,则
轴,则![]() 的方程为
的方程为![]() ,代入
,代入![]() ,得
,得![]() .
.
此时![]() ,即直线
,即直线![]() 不满足题意.
不满足题意.
若![]() 不垂直于
不垂直于![]() 轴,设
轴,设![]() 的斜率为
的斜率为![]() ,由已知得
,由已知得![]() ,
, ![]() 的方程为
的方程为![]() .
.
设![]() ,由
,由![]() 得
得![]() .
.
∴![]() .
.
∵抛物线![]() 的准线为
的准线为![]() ,
,
∴![]() ,
,
∴![]() ,解得
,解得![]() .
.
当![]() 时,
时, ![]() 化为
化为![]() ,
,
∵![]() ,∴
,∴![]() 有两个不相等实数根.
有两个不相等实数根.
∴![]() 满足题意,即直线
满足题意,即直线![]() 满足题意.
满足题意.
∴存在满足要求的直线![]() ,它的方程为
,它的方程为![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,过左焦点F且垂直于x轴的直线与椭圆
,过左焦点F且垂直于x轴的直线与椭圆![]() 相交,所得弦长为1,斜率为
相交,所得弦长为1,斜率为![]() (
(![]() )的直线
)的直线![]() 过点
过点![]() ,且与椭圆
,且与椭圆![]() 相交于不同的两点
相交于不同的两点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)在![]() 轴上是否存在点
轴上是否存在点![]() ,使得无论
,使得无论![]() 取何值,
取何值, ![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某服装厂生产一种服装,每件服装的成本为40元,出厂单价为60元,该厂为鼓励销售商订购,决定当一次订购量超过100件时,每多订购一件,订购的全部服装的出厂单价就降低0.02元,根据市场调查,销售商一次订购量不会超过500件.
(1)设一次订购量为x件,服装的实际出厂单价为P元,写出函数P=f(x)的表达式;
(2)当销售商一次订购多少件服装时,该服装厂获得的利润最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某消费品专卖店的经营资料显示如下:
①这种消费品的进价为每件14元;
②该店月销售量Q(百件)与销售价格P(元)满足的函数关系式为Q= ![]() ,点(14,22),(20,10),(26,1)在函数的图象上;
,点(14,22),(20,10),(26,1)在函数的图象上;
③每月需各种开支4400元.
(1)求月销量Q(百件)与销售价格P(元)的函数关系;
(2)当商品的价格为每件多少元时,月利润最大?并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的奇函数f(x),当x>0时,f(x)=﹣x2+2x
(1)求函数f(x)在R上的解析式;
(2)若函数f(x)在区间[﹣1,a﹣2]上单调递增,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点. 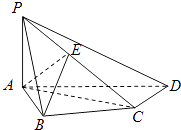
(1)证明CD⊥AE;
(2)证明PD⊥平面ABE;
(3)求二面角A﹣PD﹣C的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,过右焦点
,过右焦点![]() 垂直于
垂直于![]() 轴的直线与椭圆交于
轴的直线与椭圆交于![]() ,
, ![]() 两点且
两点且![]() ,又过左焦点
,又过左焦点![]() 任作直线
任作直线![]() 交椭圆于点
交椭圆于点![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)椭圆![]() 上两点
上两点![]() ,
, ![]() 关于直线
关于直线![]() 对称,求
对称,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A={x| ![]() <3x<9},B={x|log2x>0}.
<3x<9},B={x|log2x>0}.
(1)求A∩B和A∪B;
(2)定义A﹣B={x|x∈A且xB},求A﹣B和B﹣A.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com