
����Ŀ��ij��װ������һ�ַ�װ��ÿ����װ�ijɱ�Ϊ40Ԫ����������Ϊ60Ԫ���ó�Ϊ���������̶�����������һ�ζ���������100��ʱ��ÿ�ඩ��һ����������ȫ����װ�ij������۾ͽ���0.02Ԫ�������г����飬������һ�ζ��������ᳬ��500����
��1����һ�ζ�����Ϊx������װ��ʵ�ʳ�������ΪPԪ��д������P=f��x���ı���ʽ��
��2����������һ�ζ������ټ���װʱ���÷�װ����õ��������������ֵ��
���𰸡�
��1���⣺��һ�ζ�����Ϊx������װ��ʵ�ʳ�������ΪPԪ��
��0��x��100ʱ��P=60
��100��x��500ʱ�� ![]()
���� 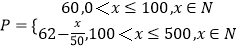
��2���⣺��������һ�ζ�����Ϊx����������õ�����ΪyԪ������ 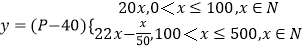
��0��x��100��x��Nʱ����֪x=100��yȡ�����ֵ2000Ԫ
��100��x��500��x��Nʱ�� ![]() ��
��
��˺�����100��x��500��x��N�ϵ�������x=500ʱ��yȡ�����ֵ6000Ԫ��
��6000��2000��
�൱������һ�ζ���500����װʱ���÷�װ����õ��������6000Ԫ
����������1�����÷ֶκ���ֱ���г������Ľ���ʽ���ɣ���2�����ã�1���г����������ֱ����ֶκ�������ֵ���Ƴ�������ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ʵ��a��b��c��d�������ĸ������е��������ǣ� ��
A.��a��b��c��0��ac��bc
B.��a��b��o��c��d��ac��bd
C.��a��b���� ![]()
D.��ac2��bc2��a��b
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
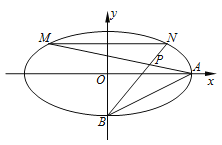
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У���֪��Բ
�У���֪��Բ![]() ����
����![]() ��
�� ![]() ��
�� ![]() �ֱ�Ϊ��Բ
�ֱ�Ϊ��Բ![]() ���ҡ��¶��㣬��
���ҡ��¶��㣬��![]() ��
��
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2�����![]() ����Բ
����Բ![]() �ڣ�����ֱ��
�ڣ�����ֱ��![]() ��
�� ![]() ��б�ʳ˻�Ϊ
��б�ʳ˻�Ϊ![]() ����ֱ��
����ֱ��![]() ��
�� ![]() �ֱ���Բ
�ֱ���Բ![]() �ڵ�
�ڵ�![]() ��
�� ![]() ��
��
(i) ��![]() ��
�� ![]() ����
����![]() ��Գƣ���ֱ��
��Գƣ���ֱ��![]() ��б�ʣ�
��б�ʣ�
(ii) ��֤�� ![]() �������
�������![]() �������ȣ�
�������ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ⳤΪ1��������ABCD��A1B1C1D1�У���E��F�ֱ�����BC��CC1���е㣬P�Dz���BCC1B1��һ�㣬��A1P��ƽ��AEF�����߶�A1P���ȵ�ȡֵ��Χ�� �� 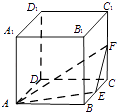
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
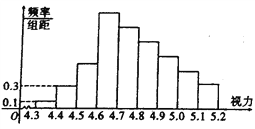
����Ŀ��ͳ��ȫ������ѧ��������������õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ�����ڲ������������ݶ�ʧ����֪��ǰ4���Ƶ�ʳɵȱ����У���6���Ƶ�ʳɵȲ�����.
�������������[4.7,4.8]��Ƶ�ʣ�
�����ִ�ȫ���ĸ���ѧ��������س�ȡ4�ˣ���![]() ��ʾ������[4.3,4.7]��ѧ��������д��
��ʾ������[4.3,4.7]��ѧ��������д��![]() �ķֲ��У������
�ķֲ��У������![]() �������뷽��.
�������뷽��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����F��x��=g��x��+h��x��=ex �� ��g��x����h��x���ֱ���R�ϵ�ż�������溯�������������x�ʣ�0��+�ޣ�������ʽg��2x����ah��x�����������ʵ��a��ȡֵ��Χ�ǣ� ��
A.�����ޣ�2 ![]() ]
]
B.�����ޣ�2 ![]() ��
��
C.�����ޣ�2]
D.�����ޣ�2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=��3x2+a��6��a��x+c��
��1����c=19ʱ�������a�IJ���ʽf��1����0��
��2��������x�IJ���ʽf��x����0�Ľ⼯�ǣ���1��3������ʵ��a��c��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �Ķ���Ϊԭ��
�Ķ���Ϊԭ��![]() ������ΪԲ
������ΪԲ![]() ��Բ��
��Բ��![]() .������
.������![]() ��ֱ��
��ֱ��![]() ��������
��������![]() ��
��![]() ���㣬��Բ
���㣬��Բ![]() ��
��![]() ���㣬
���㣬 ![]() �ڵ�һ���ޣ�
�ڵ�һ���ޣ� ![]() �ڵ�������.
�ڵ�������.
��1����������![]() �ķ��̣�
�ķ��̣�
��2���Ƿ����ֱ��![]() ��ʹ
��ʹ![]() ��
��![]() ��
��![]() �ĵȲ���������ڣ���ֱ��
�ĵȲ���������ڣ���ֱ��![]() �ķ��̣��������ڣ���˵������.
�ķ��̣��������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���мס��������������ѧ���ԣ����մ��ڵ���120��Ϊ���㣬120������Ϊ������ͳ�Ƴɼ��õ�����![]() ������������λ���ˣ�.
������������λ���ˣ�.

��֪��ȫ��105���������ȡ1�˳ɼ�������ĸ���Ϊ![]() .
.
��1������������![]() �������������ݱ��������жϣ��Ƿ���
�������������ݱ��������жϣ��Ƿ���![]() �İ�����Ϊ���ɼ���༶�й�ϵ����
�İ�����Ϊ���ɼ���༶�й�ϵ����
��2�����װ�����ѧ����������6����Ů��4�����ִ������ѡ��3��ѧ���μ�ȫ����ѧ�������DzμӾ�������������Ϊ![]() ����
����![]() �ķֲ���������.
�ķֲ���������.
���� 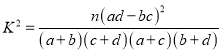
| 0.15 | 0.10 | 0.050 | 0.010 |
| 2.072 | 2.706 | 3.841 | 6.635 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com