练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知平面，是两个相交平面，其中，则

    A.平面内一定能找到与平行的直线

    B.平面内一定能找到与垂直的直线

    C.若平面内有一条直线与平行，则该直线与平面平行

    D.若平面内有无数条直线与垂直，则平面与平面垂直

    【答案】B

    【解析】

    在A中，当与，的交线相交时，内不能找到与平行的直线；在B中，内一定能找到与垂直的直线；在C中，该直线与平行或该直线在内；在D中，与不一定垂直，即可得到答案.

    由题意，平面，是两个相交平面，其中，

    在A中，当与，的交线相交时，内不能找到与平行的直线，所以不正确；

    在B中，由直线与平面的位置关系，可知内一定能找到与垂直的直线，所以是正确的；在C中，平面内有一条直线与平行，该直线与平行或该直线在内，所以不正确；在D中，平面内有无数条直线与垂直，则与不一定垂直，所以不正确，

    故选B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

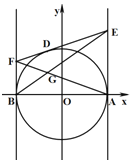
    【题目】如图所示，圆O：，，，D为圆O上任意一点，过D作圆O的切线分别交直线和于E，F两点，连AF，BE交于点G，若点G形成的轨迹为曲线C．

    记AF，BE斜率分别为，，求的值并求曲线C的方程；

    设直线l：与曲线C有两个不同的交点P，Q，与直线交于点S，与直线交于点T，求的面积与面积的比值的最大值及取得最大值时m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列说法中错误的是__________（填序号）

    ①命题“，有”的否定是“”，有”；

    ②已知， ， ，则的最小值为；

    ③设，命题“若，则”的否命题是真命题；

    ④已知， ，若命题为真命题，则的取值范围是.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，．

    （1）判断的单调性，并证明之；

    （2）若存在实数，，使得函数在区间上的值域为，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若的展开式中，第二、三、四项的二项式系数成等差数列．

    （1）求的值；

    （2）此展开式中是否有常数项，为什么？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四边形ABCD是平行四边形，点E，F，G分别为线段BC，PB，AD的中点．

    （1）证明：EF∥平面PAC；

    （2）证明：平面PCG∥平面AEF；

    （3）在线段BD上找一点H，使得FH∥平面PCG，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】近年来，某市为响应国家号召，大力推行全民健身运动，加强对市内各公共体育运动设施的维护，几年来，经统计，运动设施的使用年限x（年）和所支出的维护费用y（万元）的相关数据如图所示，根据以往资料显示y对x呈线性相关关系。

    （1）求出y关于x的回归直线方程少

    （2）试根据（1）中求出的回归方程，预测使用年限至少为几年时，维护费用将超过100万元？

    参考公式：对于一组数据（x1，yl），（x2，y2），…，（xn，Yn），其回归方程的斜率和截距的最小二乘估计分别为

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）讨论的单调性；

    （2）若存在实数，使得，求正实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知， ， ．

    （1）当时，试比较与的大小关系；

    （2）猜想与的大小关系，并给出证明．

    查看答案和解析>>

    同步练习册答案