
【题目】已知函数f(x)=|2x﹣1|,当a<b<c时,f(a)>f(c)>f(b),那么正确的结论是( )
A.2a>2b
B.2a>2c
C.2﹣a<2c
D.2a+2c<2
【答案】D
【解析】∵函数f(x)=|2x﹣1|,
∴f(x)=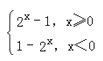 .
.
画出函数图象如下图所示: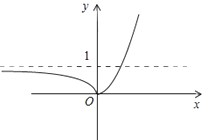
可知:函数f(x)在区间(﹣∞,0)上单调递减,在区间(0,+∞)上单调递增.
当0≤a<b<c时,f(x)在区间(0,+∞)上单调递增,不满足f(a)>f(b)>f(c),因此必有a<0.
当a<0<c时,1﹣2a>2c﹣1,化为2a+2c<2;
当a<b<c≤0时,f(x)在区间(﹣∞,0]上单调递减.
∴1>1﹣2a>1﹣2c≥0,
∴2c≤1,2a<1,
∴2a+2c<2.
综上可知:D一定正确.
故选:D.
函数f(x)=|2x﹣1|,可得f(x)=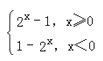 . 画出函数图象.利用函数图象的单调性和已知条件可得:当0≤a<b<c时,不满足f(a)>f(b)>f(c),因此必有a<0.当a<0<c时,1﹣2a>2c﹣1,化为2a+2c<2;当a<b<c≤0时,f(x)在区间(﹣∞,0]上也满足2a+2c<2.
. 画出函数图象.利用函数图象的单调性和已知条件可得:当0≤a<b<c时,不满足f(a)>f(b)>f(c),因此必有a<0.当a<0<c时,1﹣2a>2c﹣1,化为2a+2c<2;当a<b<c≤0时,f(x)在区间(﹣∞,0]上也满足2a+2c<2.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:高中数学 来源: 题型:
【题目】在四棱柱ABCD-A1B1C1D1中,![]() ,平面BB1C1C
,平面BB1C1C![]() 底面ABCD,点
底面ABCD,点![]() 、F分别是线段
、F分别是线段![]() 、BC的中点.
、BC的中点.
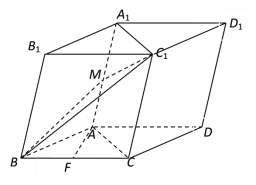
(1)求证:AF//平面![]() ;
;
(2)求证:平面BB1C1C⊥平面![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系![]() 的原点为极点,
的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位.若直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位.若直线![]() 的参数方程为
的参数方程为![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(I)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(II)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,若
两点,若![]() 点的直角坐标为
点的直角坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】辽宁号航母纪念章从2012年10月5日起开始上市,通过市场调查,得到该纪念章每![]() 枚的市场价
枚的市场价![]() (单位:元)与上市时间
(单位:元)与上市时间![]() (单位:天)的数据如下:
(单位:天)的数据如下:
上市时间 |
|
|
|
市场价 |
|
|
|
(1)根据上表数据,从下列函数中选取一个恰当的函数描述辽宁号航母纪念章的市场价![]() 与上市时间
与上市时间![]() 的变化关系:①
的变化关系:①![]() ;②
;②![]() ;③
;③![]() ;
;
(2)利用你选取的函数,求辽宁号航母纪念章市场价最低时的上市天数及最低的价格;
(3)设你选取的函数为![]() ,若对任意实数
,若对任意实数![]() ,关于
,关于![]() 的方程
的方程![]() 恒有个想异实数根,求
恒有个想异实数根,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列五个命题:
①函数f(x)=2a2x-1-1的图象过定点(![]() ,-1);
,-1);
②已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=x(x+1),若f(a)=-2则实数a=-1或2.
③若loga![]() >1,则a的取值范围是(
>1,则a的取值范围是(![]() ,1);
,1);
④若对于任意x∈R都f(x)=f(4-x)成立,则f(x)图象关于直线x=2对称;
⑤对于函数f(x)=lnx,其定义域内任意x1≠x2都满足f(![]() )≥
)≥![]()
其中所有正确命题的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的标准方程为
的标准方程为![]() ,
,![]() 为圆
为圆![]() 上的动点,直线
上的动点,直线![]() 的方程为
的方程为![]() ,动点
,动点![]() 在直线
在直线![]() 上.
上.
(1)求![]() 的最小值,并求此时点
的最小值,并求此时点![]() 的坐标;
的坐标;
(2)若![]() 点的坐标为
点的坐标为![]() ,过
,过![]() 作直线与圆
作直线与圆![]() 交于
交于![]() ,
,![]() 两点,当
两点,当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 其图像的一个对称中心是
其图像的一个对称中心是![]() 将
将![]() 的图像向左平移
的图像向左平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图像。
的图像。
(1)求函数![]() 的解析式;
的解析式;
(2)若对任意![]() 当
当![]() 时,都有
时,都有![]() 求实数
求实数![]() 的最大值;
的最大值;
(3)若对任意实数![]() 在
在![]() 上与直线
上与直线![]() 的交点个数不少于6个且不多于10个,求正实数
的交点个数不少于6个且不多于10个,求正实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,E,F分别是PB,PD的中点.
(I)求证:PB∥平面FAC;
(II)求三棱锥P-EAD的体积;
(III)求证:平面EAD⊥平面FAC.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com