
【题目】在直角坐标系![]() 中,动圆
中,动圆![]() 与圆
与圆![]() 外切,且圆
外切,且圆![]() 与直线
与直线![]() 相切,记动圆圆心
相切,记动圆圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)设过定点![]() 的动直线
的动直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,试问:在曲线
两点,试问:在曲线![]() 上是否存在点
上是否存在点![]() (与
(与![]() 两点相异),当直线
两点相异),当直线![]() 的斜率存在时,直线
的斜率存在时,直线![]() 的斜率之和为定值?若存在,求出点
的斜率之和为定值?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)答案见解析.
;(2)答案见解析.
【解析】
(1)设![]() ,圆
,圆![]() 的半径为
的半径为![]() ,由动圆
,由动圆![]() 与圆
与圆![]() 外切,可得
外切,可得![]() ,又动圆
,又动圆![]() 与直线
与直线![]() 相切,所以
相切,所以![]() ,两式结合消去
,两式结合消去![]() 即可得结果;(2)设出
即可得结果;(2)设出![]() 的坐标,
的坐标,
直线方程为![]() ,联立直线与抛物线方程消去
,联立直线与抛物线方程消去![]() 可得关于
可得关于![]() 的一元二次方程,由韦达定理、斜率公式可得
的一元二次方程,由韦达定理、斜率公式可得![]() ,
,![]() ,化为
,化为![]() ,由
,由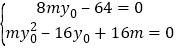 可得结果.
可得结果.
(1)设P(x,y),圆P的半径为r,
因为动圆P与圆Q:(x-2)2+y2=1外切,
所以![]() ,①
,①
又动圆P与直线x=-1相切,所以r=x+1,②
由①②消去r得y2=8x,
所以曲线C的轨迹方程为y2=8x.
(2)假设存在曲线C上的点M满足题设条件,不妨设M(x0,y0),A(x1,y1),B(x2,y2),
则![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
所以![]() ,③
,③
显然动直线l的斜率存在且非零,设l:x=ty-2,
联立方程组![]() ,消去x得y2-8ty+16=0,
,消去x得y2-8ty+16=0,
由Δ>0得t>1或t<-1,
所以y1+y2=8t,y1y2=16,且y1≠y2,
代入③式得![]() ,令
,令![]() (m为常数),
(m为常数),
整理得![]() ,④
,④
因为④式对任意t∈(-∞,-1)∪(1,+∞)恒成立,
所以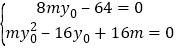 ,
,
所以![]() 或
或![]() ,即M(2,4)或M(2,-4),
,即M(2,4)或M(2,-4),
即存在曲线C上的点M(2,4)或M(2,-4)满足题意.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)若函数![]() ,求函数
,求函数![]() 的极值;
的极值;
(2)讨论函数![]() 在定义域内极值点的个数;
在定义域内极值点的个数;
(3)设直线![]() 为函数
为函数![]() 的图象上一点
的图象上一点![]() 处的切线,证明:在区间
处的切线,证明:在区间![]() 上存在唯一的
上存在唯一的![]() ,使得直线
,使得直线![]() 与曲线
与曲线![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程与直线
的普通方程与直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
, ![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有四个小球,分别写有“美、丽、中、国”四个字,有放回地从中任取一个小球,直到“中”“国”两个字都取到就停止,用随机模拟的方法估计恰好在第三次停止的概率.利用电脑随机产生0到3之间取整数值的随机数,分别用0,1,2,3代表“中、国、美、丽”这四个字,以每三个随机数为一组,表示取球三次的结果,经随机模拟产生了以下18组随机数:
232 321 230 023 123 021 132 220 001
231 130 133 231 031 320 122 103 233
由此可以估计,恰好第三次就停止的概率为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到频数分布表和频率分布直方图如下.
组号 | 分组 | 频数 |
1 | [0,2) | 6 |
2 | [2,4) | 8 |
3 | [4,6) | 17 |
4 | [6,8) | 22 |
5 | [8,10) | 25 |
6 | [10,12) | 12 |
7 | [12,14) | 6 |
8 | [14,16) | 2 |
9 | [16,18) | 2 |
合计 | 100 |

(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的频率;
(2)求频率分布直方图中的a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从一张半径为3的圆形铁皮中裁剪出一块扇形铁皮(如图1阴影部分),并卷成一个深度为![]() 米的圆锥筒(如图2).若所裁剪的扇形铁皮的圆心角为
米的圆锥筒(如图2).若所裁剪的扇形铁皮的圆心角为![]() .
.
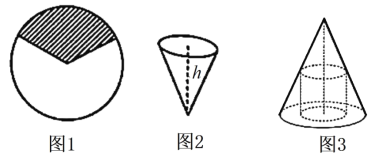
(1)求圆锥筒的容积;
(2)在(1)中的圆锥内有一个底面圆半径为![]() 的内接圆柱(如图3),求内接圆柱侧面积最大时
的内接圆柱(如图3),求内接圆柱侧面积最大时![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com