Question

14、如图，在正方体ABCD-A₁B₁C₁D₁中，E为DD₁的中点．求证：
（1）BD₁∥平面EAC；
（2）平面EAC⊥平面AB₁C．

Answer 1

分析：（1）连接BD，交AC于O．连接EO，BD₁．根据中位线可知BD₁∥OE，又OE?平面EAC，BD₁?平面EAC，根据线面平行的判定定理可知BD₁∥平面EAC；
（2）根据BB₁⊥AC，BD⊥AC，BB₁∩BD=B，满足线面垂直的判定定理，则AC⊥平面BB₁D₁D，又BD₁?平面BB₁D₁D则BD₁⊥AC，同理BD₁⊥AB₁，从而BD₁⊥平面AB₁C．根据（1）可得BD₁∥OE，从而EO⊥平面AB₁C，又EO?平面EAC，根据面面垂直的判定定理可知平面EAC⊥平面AB₁C．

解答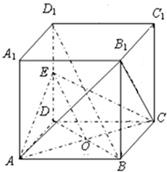：证明：（1）连接BD，交AC于O．连接EO，BD₁．（2分）
因为E为DD₁的中点，所以BD₁∥OE．（5分）
又OE?平面EAC，BD₁?平面EAC，
所以BD₁∥平面EAC；（7分）
（2）∵BB₁⊥AC，BD⊥AC．∴AC⊥平面BB₁D₁D
又BD₁?平面BB₁D₁D∴BD₁⊥AC．（10分）
同理BD₁⊥AB₁，∴BD₁⊥平面AB₁C．（12分）
由（1）得BD₁∥OE，∴EO⊥平面AB₁C．
又EO?平面EAC，∴平面EAC⊥平面AB₁C．（14分）

点评：本题考查直线与平面平行的判定，以及平面与平面垂直的判定，同时考查学生空间想象能力，逻辑思维能力，是中档题．