
【题目】已知圆M过C(1,-1),D(-1,1)两点,且圆心M在x+y-2=0上.
(1)求圆M的方程;
(2)设点P是直线3x+4y+8=0上的动点,PA,PB是圆M的两条切线,A,B为切点,求四边形PAMB面积的最小值.
【答案】(1)(x﹣1)2+(y﹣1)2=4.(2)2![]() .
.
【解析】
试题分析:(1)设出圆的标准方程,利用圆M过两点C(1,-1)、D(-1,1)且圆心M在直线x+y-2=0上,建立方程组,即可求圆M的方程;
(2)四边形PAMB的面积为S=2![]() ,因此要求S的最小值,只需求|PM|的最小值即可,即在直线3x+4y+8=0上找一点P,使得|PM|的值最小,利用点到直线的距离公式,即可求得结论.
,因此要求S的最小值,只需求|PM|的最小值即可,即在直线3x+4y+8=0上找一点P,使得|PM|的值最小,利用点到直线的距离公式,即可求得结论.
试题解析:
(1) 设圆M的方程为(x-a)2+(y-b)2=r2(r>0),
根据题意得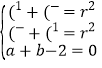
解得a=b=1,r=2.
故所求圆M的方程为(x-1)2+(y-1)2=4.
(2) 由题知,四边形PA′MB′的面积为S=S△PA′M+S△PB′M=![]() |A′M||PA′|+
|A′M||PA′|+![]() |B′M||PB′|.
|B′M||PB′|.
又|A′M|=|B′M|=2,|PA′|=|PB′|,
所以S=2|PA′|.
而|PA′|=![]() .
.
即S=2![]() .
.
因此要求S的最小值,只需求|PM|的最小值即可,即在直线3x+4y+8=0上找一点P,使得|PM|的值最小,
所以|PM|min=![]() ,
,
所以四边形PA′MB′面积的最小值为S=2![]() =2
=2![]() =2
=2![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,AB=AC=1,∠BAC=90°,异面直线A1B与B1C1所成的角为60°.
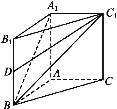
(1)求该三棱柱的体积;
(2)设D是BB1的中点,求DC1与平面A1BC1所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将菱形ABCD沿对角线BD折起,使得C点至C′,E点在线段AC′上,若二面角A﹣BD﹣E与二面角E﹣BD﹣C′的大小分别为15°和30°,则![]() __.
__.
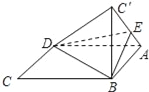
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T.其
范围为[0,10],分别有五个级别:T∈[0,2)畅通;T∈[2,4)基本畅通; T∈[4,6)轻度拥堵; T∈[6,8)中度拥堵;T∈[8,10]严重拥堵,晚高峰时段(T≥2),从某市交通指挥中心选取了市区20个交通路段,依据其交通指数数据绘制的部分直方图如图所示.
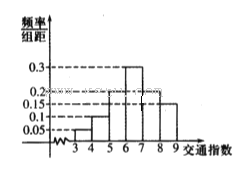
(1)请补全直方图,并求出轻度拥堵、中度拥堵、严重拥堵路段各有多少个?
(2)用分层抽样的方法从交通指数在[4,6),[6,8),[8,l0]的路段中共抽取6个路段,求依次抽取的三个级别路段的个数;
(3)从(2)中抽出的6个路段中任取2个,求至少一个路段为轻度拥堵的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,AB∥CD,且∠BAP=∠CDP=90°.(12分) 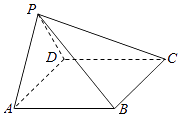
(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,∠APD=90°,求二面角A﹣PB﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn.已知2Sn=3n+3.
(1)求{an}的通项公式;
(2)若数列{bn}满足anbn=log3an,求{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中, ![]() 且
且![]() 底面
底面![]() ,D是PC的中点,已知
,D是PC的中点,已知![]() ,AB=2,AC=
,AB=2,AC=![]() ,PA=2.
,PA=2.
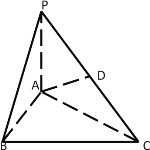
(1)求三棱锥P-ABC的体积
(2)求异面直线BC与AD所成角的余弦值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com