
已知椭圆 过点
过点 ,且离心率为
,且离心率为 .斜率为
.斜率为 的直线
的直线 与椭圆
与椭圆 交于
交于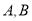 两点,以
两点,以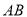 为底边作等腰三角形,顶点为
为底边作等腰三角形,顶点为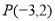 .
.
(1)求椭圆 的方程;
的方程;
(2)求 的面积.
的面积.
(1)  ; (2)
; (2) 
【解析】
试题分析:(1)根据题意可列方程组 ,进而可求解
,进而可求解 的值.
的值.
(2) 设直线l的方程为 .联立直线与椭圆的方程可得:
.联立直线与椭圆的方程可得: ,①
,①
利用 ,因此要先确定直线AB的方程和点P到直线AB的距离.设A、B的坐标分别为
,因此要先确定直线AB的方程和点P到直线AB的距离.设A、B的坐标分别为 AB中点为E
AB中点为E ,则
,则 .
.
因为AB是等腰△ 的底边,所以PE⊥AB.所以PE的斜率
的底边,所以PE⊥AB.所以PE的斜率 ,解得m=2.
,解得m=2.
此时方程①为 ,解得
,解得 ,所以
,所以 ,所以|AB|=
,所以|AB|= . 此时,点P(-3,2)到直线AB:
. 此时,点P(-3,2)到直线AB: 的距离
的距离 ,所以S=
,所以S= .
.
(1)由已知得 . ( 2分)
. ( 2分)
解得 .又
.又 ,所以椭圆G的方程为
,所以椭圆G的方程为 . (4分)
. (4分)
(2)设直线l的方程为 .
.
由 得
得 . ① 6分
. ① 6分
设A、B的坐标分别为 AB中点为E
AB中点为E ,
,
则 . ( 8分),
. ( 8分),
因为AB是等腰△ 的底边,
的底边,
所以PE⊥AB.所以PE的斜率 ,解得m=2. ( 10分)
,解得m=2. ( 10分)
此时方程①为 ,解得
,解得 ,所以
,所以 ,所以|AB|=
,所以|AB|= . 此时,点P(-3,2)到直线AB:
. 此时,点P(-3,2)到直线AB: 的距离
的距离 , 所以△
, 所以△ 的面积S=
的面积S= . (12分)
. (12分)
考点:椭圆方程、性质;直线与椭圆的位置关系,两点间的距离公式,点到直线的距离公式,三角形面积公式.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源:2015届吉林省长春市新高三起点调研考试文科数学试卷(解析版) 题型:解答题
如图,椭圆
 的左焦点为
的左焦点为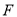 ,过点
,过点 的直线交椭圆于
的直线交椭圆于 两点.
两点.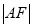 的最大值是
的最大值是 ,
, 的最小值是
的最小值是 ,满足
,满足 .
.
(1) 求该椭圆的离心率;
(2) 设线段 的中点为
的中点为 ,
, 的垂直平分线与
的垂直平分线与 轴和
轴和 轴分别交于
轴分别交于 两点,
两点, 是坐标原点.记
是坐标原点.记 的面积为
的面积为 ,
,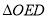 的面积为
的面积为 ,求
,求 的取值范围.
的取值范围.

查看答案和解析>>
科目:高中数学 来源:2015届吉林省长春市高二下学期期末考试理科数学试卷(解析版) 题型:选择题
设某大学的女生体重 (单位:
(单位: )与身高
)与身高 (单位:
(单位: )具有线性相关关系,根据一组样本数据
)具有线性相关关系,根据一组样本数据 (
( ),用最小二乘法建立的回归方程为
),用最小二乘法建立的回归方程为 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A. 与
与 具有正的线性相关关系
具有正的线性相关关系
B.回归直线过样本点的中心
C.若该大学某女生身高增加 ,则其体重约增加
,则其体重约增加
D.若该大学某女生身高为 ,则可断定其体重为
,则可断定其体重为
查看答案和解析>>
科目:高中数学 来源:2015届吉林省长春市高二下学期期末考试文科数学试卷(解析版) 题型:选择题
在△ 中,内角
中,内角 的对边分别为
的对边分别为 ,若
,若 ,
, ,
, ,则这样的三角形有( )
,则这样的三角形有( )
A.0个 B.两个 C.一个 D.至多一个
查看答案和解析>>
科目:高中数学 来源:2015届吉林省长春市高二下学期期中考试理科数学试卷(解析版) 题型:填空题
将一列有规律的正整数排成一个三角形数阵(如图):根据排列规律,数阵中第12行的从左至右的第4个数是_______.

查看答案和解析>>
科目:高中数学 来源:2015届吉林省长春市高二下学期期中考试文科数学试卷(解析版) 题型:填空题
为了测算如图阴影部分的面积,作一个边长为6的正方形将其包含在内,并向正方形内随机投掷800个点,已知恰有200个点落在阴影部分内,据此,可估计阴影部分的面积是 .

查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁省沈阳市高二上学期10月月考数学试卷(解析版) 题型:解答题
(本小题满分12分)设A(x1,y1),B(x2,y2)是函数f(x)= 的图象上任意两点,且
的图象上任意两点,且 ,已知点M的横坐标为
,已知点M的横坐标为 .
.
求证:M点的纵坐标为定值;
若Sn=f( ∈N*,且n≥2,求Sn;
∈N*,且n≥2,求Sn;
已知an= ,其中n∈N*.
,其中n∈N*.
Tn为数列{an}的前n项和,若Tn<λ(Sn+1+1)对一切n∈N*都成立,试求λ的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com