
(本小题满分12分)设A(x1,y1),B(x2,y2)是函数f(x)= 的图象上任意两点,且
的图象上任意两点,且 ,已知点M的横坐标为
,已知点M的横坐标为 .
.
求证:M点的纵坐标为定值;
若Sn=f( ∈N*,且n≥2,求Sn;
∈N*,且n≥2,求Sn;
已知an= ,其中n∈N*.
,其中n∈N*.
Tn为数列{an}的前n项和,若Tn<λ(Sn+1+1)对一切n∈N*都成立,试求λ的取值范围.
(1)见解析;(2)Sn= ;(3)(
;(3)( +∞).
+∞).
【解析】
试题分析:(1)依题意M是AB的中点,得x1+x2=1,而y=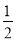 (y1+y2)=
(y1+y2)= 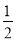 [f(x1)+f(x2)]利用解析式可得y=
[f(x1)+f(x2)]利用解析式可得y=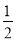 ,即纵坐标为定值;(2)由(1)知x1+x2=1,则f(x1)+f(x2)=1,而Sn=f(
,即纵坐标为定值;(2)由(1)知x1+x2=1,则f(x1)+f(x2)=1,而Sn=f( 观察特点,利用倒序相加求和可得Sn=
观察特点,利用倒序相加求和可得Sn= ;(3)由(2)可得
;(3)由(2)可得 ,利用裂项相消求和可得
,利用裂项相消求和可得 ,代入Tn<λ(Sn+1+1)转化为恒成立问题解决,从而得λ>
,代入Tn<λ(Sn+1+1)转化为恒成立问题解决,从而得λ>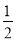 .
.
试题解析:(1)证明:∵ ∴M是AB的中点.设M点的坐标为(x,y),
∴M是AB的中点.设M点的坐标为(x,y),
由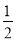 (x1+x2)=x=
(x1+x2)=x=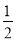 ,得x1+x2=1,则x1=1-x2或x2=1-x1.
,得x1+x2=1,则x1=1-x2或x2=1-x1.
而y=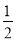 (y1+y2)=
(y1+y2)= 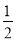 [f(x1)+f(x2)] =
[f(x1)+f(x2)] =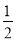 (
(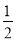 +log2
+log2
=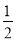 (1+log2
(1+log2 =
=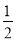 (1+log2
(1+log2
=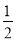 (1+log2
(1+log2
∴M点的纵坐标为定值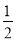 .
.
(2)由(1)知x1+x2=1,f(x1)+f(x2)=y1+y2=1,
Sn=f(
Sn=f( ,
,
两式相加得:2Sn=[f(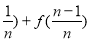 )+[f(
)+[f( )+…+[f(
)+…+[f( )
)
= ∴Sn=
∴Sn= (n≥2,n∈N*).
(n≥2,n∈N*).
(3)当n≥2时,an=
Tn=a1+a2+a3+…+an= [(
[( ) =
) = (
(
由Tn<λ(Sn+1+1)得 <λ·
<λ· ∴λ>
∴λ>
∵n+ ≥4,当且仅当n=2时等号成立,∴
≥4,当且仅当n=2时等号成立,∴
因此λ>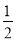 ,即λ的取值范围是(
,即λ的取值范围是( +∞).
+∞).
考点:函数和数列的综合问题


科目:高中数学 来源:2015届吉林省长春市高二下学期期中考试理科数学试卷(解析版) 题型:解答题
已知椭圆 过点
过点 ,且离心率为
,且离心率为 .斜率为
.斜率为 的直线
的直线 与椭圆
与椭圆 交于
交于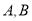 两点,以
两点,以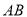 为底边作等腰三角形,顶点为
为底边作等腰三角形,顶点为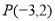 .
.
(1)求椭圆 的方程;
的方程;
(2)求 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁省高二第一次月考数学试卷(解析版) 题型:选择题
已知函数 的值域为[0,+∞),若关于x的不等式f(x)<c的解集为(m,m+6),则实数c的值为( )
的值域为[0,+∞),若关于x的不等式f(x)<c的解集为(m,m+6),则实数c的值为( )
A. 7 B. 8 C. 9 D. 10
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁省高二第一次月考数学试卷(解析版) 题型:选择题
在等差数列{an}中,a1=-28,公差d=4,若前n项和 取得最小值,则n的值为
取得最小值,则n的值为
A.7 B.8 C.7或8 D.8或9
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁省高一上学期10月月考数学试卷(解析版) 题型:填空题
设全集U=R,集合A={x|x2?x?2= 0},B={y|y=x+1,x?A},则 =__________.
=__________.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁省分校高二10月月考数学试卷(解析版) 题型:填空题
在数列{an}中,a1=1,an+1= (n∈N*),则这个数列的通项公式是
(n∈N*),则这个数列的通项公式是 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com